Archive for the ‘Scientists & History’ Category
Aug
20
Posted by jns on
August 20, 2009
 This is the youthful Galileo Galilei (1564–1642), who established the intellectual starting point for this short discussion.
This is the youthful Galileo Galilei (1564–1642), who established the intellectual starting point for this short discussion.
In Galileo’s day [c. 1610], the study of astronomy was used to maintain and reform the calendar. Sufficiently advanced students of astronomy made horoscopes; the alignment of the stars was believed to influence everything from politics to health.
[David Zax, "Galileo's Vision", Smithsonian Magazine, August 2009.*]
Galileo published The Starry Messenger (Sidereus Nuncius), the book in which he reported his discovery of four new planets (i.e., moons) apparently orbiting Jupiter, in 1610. This business of looking at things and reporting on observations just didn’t fit well with the prevailing Aristotelian view of nature and the way things were done.
Some of his contemporaries refused to even look through the telescope at all, so certain were they of Aristotle’s wisdom. “These satellites of Jupiter are invisible to the naked eye and therefore can exercise no influence on the Earth, and therefore would be useless, and therefore do not exist,” proclaimed nobleman Francesco Sizzi. Besides, said Sizzi, the appearance of new planets was impossible—since seven was a sacred number: “There are seven windows given to animals in the domicile of the head: two nostrils, two eyes, two ears, and a mouth….From this and many other similarities in Nature, which it were tedious to enumerate, we gather that the number of planets must necessarily be seven.”
[link as above]
Science as a an empirical pursuit was still a new idea, quite evidently.
At the time it was understood, for various “obvious” reasons (one of them apparently being that they could be seen), that the planets and the stars in the nearby “heavens” (rather literally) influenced things on Earth. There was no known reason why or how, but this wasn’t a big issue because causality‡ didn’t play a very large role in scientific explanations of the day. Recall, for instance, that heavier objects rushed faster to tall to Earth because it was their nature to do so.
What I suddenly realized awhile back (I was reading the book by Robert P, Crease, Great Equations, but I don’t really remember what prompted the thoughts) is the following.
Received mysticism today claims that astrology, the practice of divination through observation of the motions of the planets, operates through the agency of some unknown, mysterious force as yet unknown to science. Science doesn’t know everything!
But this is wrong. In the time of Galileo there was no known “force” to serve as the “cause” for the planets’ effect on human life, but it seemed quite reasonable. In fact, the idea of “force” wasn’t yet in the mental frame. The notion of “force” as it is familiar to us today only began to take shape with the work of Isaac Newton c. 1687, when he published his Philosophiae Naturalis Principia Mathematica, which contained his theories of mechanics and gravitation, theories where the idea of “force” began to take shape, and to develop the ideas of causality.
But the notion that there is no known mechanism through which astrology might work we now see is wrong. The mechanism, arrived at by Newton, which handily explained virtually everything about how the planets moved and exerted their influence on everything in the known universe, was that of universal gravitation.
The one thing that universal gravitation did not explain was astrology. But even worse, this brilliant theory showed that the universal force behind planetary interaction and influence was much, much too small to have any influence whatsoever on humans and their lives.
Newton debunked astrology over 300 years ago by discovering its mechanism and finding that it could not possibly have the influence that its adherents claimed.
Some people, of course, are a little slow to catch up with modern developments.
———-
* This is an interesting article that accompanies a virtual exhibit, “Galileo’s Instruments of Discovery“, adjunct to a physical exhibit at the Franklin Institute (Philadelphia).
‡ Perhaps it would be more accurate to say that our modern notion of causes was quite a bit different from 15th century notions of causes.
May
27
Posted by jns on
May 27, 2009
 This* is Scottish physicist James Clerk Maxwell (1831–1879). He did significant work in several fields (including statistical physics and thermodynamics, in which I used to research) but his fame is associated with his electromagnetic theory. Electromagnetism combined the phenomena of electricity and magnetism into one, unified field theory. Unified field theories are still all the rage. It was a monumental achievement, but there was also a hidden bonus in the equations. We’ll get to that.
This* is Scottish physicist James Clerk Maxwell (1831–1879). He did significant work in several fields (including statistical physics and thermodynamics, in which I used to research) but his fame is associated with his electromagnetic theory. Electromagnetism combined the phenomena of electricity and magnetism into one, unified field theory. Unified field theories are still all the rage. It was a monumental achievement, but there was also a hidden bonus in the equations. We’ll get to that.
He published his equations in the second volume of his A Treatise on Electricity & Magnetism, in 1873. I think we should look at them because they’re pretty; I suspect they’re even kind of pretty regardless of whether the math symbols convey significant meaning to you. There are four (which you may not see in Bloglines, which doesn’t render tables properly for me):
I don’t want to explain much detail at all because it’s not necessary for what we’re talking about, but there are a few fun things to point out. The E is the electric field; the B is the magnetic field.
The two equations on the top say that electric fields are caused by electric charges, but magnetic fields don’t have “magnetic charges” (aka “magnetic monopoles”) as their source. The top right equation gets changed if a magnetic monopole is ever found.
The two equations on the bottom say that electric fields can be caused by magnetic fields that vary in time; likewise, magnetic fields can be caused by electric fields that vary in time. These are the equations that unify electricity and magnetism since, as you can easily see, the behavior of each depends on the other.
There’s one more equation to look at. A few simple manipulations with some of the equations above lead to this result:
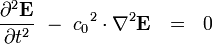
This equation has the form of a wave equation, so called because propagating waves are solutions to the equation. Maxwell obtained this result and then made a key identification. Just from its form the mathematician can see that the waves that solve this equation travel with a speed given by 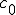 , which is related to the product of the physical constants
, which is related to the product of the physical constants  and
and 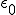 that appeared in the earlier equations.
that appeared in the earlier equations.
The values of these were known at the time and Maxwell made the thrilling discovery that this speed
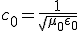
was remarkably close to the measured value of the speed of light. He concluded that light was a propagating electromagnetic wave. He was right.
That’s fine for the electromagnetism part. What’s the relationship with relativity? Let’s keep it simple and suggestive. You know from the popular lore that Einstein came up with the ideas of special relativity from thinking about traveling at the speed of light, and that the speed of light (in vacuum) is a “universal speed limit”. Only light — electromagnetic waves or photons depending on how your experiment is measuring it/them — travels at the speed of light.†
In fact, Einstein’s relativity paper (published as “Zur Elektrodynamik bewegter Körper”, in Annalen der Physik. 17:891, 1905) was titled “On the Electrodynamics of Moving Bodies”. (Read an English version here; there are no equations at the start, so read the beginning and be surprised how familiar it sounds.) That’s suggestive, don’t you think?
Speaking of special relativity, you’ve no doubt heard of the idea of an “inertial reference frame”, a concept that is central to special relativity. But, what exactly is an “inertial reference frame”?
I’m so glad you asked, since that was half the point of this post anyway. You surely realized by this time that Maxwell was partly a pretext. For our entertainment and enlightenment today we have educational films.
First, a quick introduction to the “PSSC Physics” course. From the MIT Archives:
In 1956 a group of university physics professors and high school physics teachers, led by MIT’s Jerrold Zacharias and Francis Friedman, formed the Physical Science Study Committee (PSSC) to consider ways of reforming the teaching of introductory courses in physics. Educators had come to realize that textbooks in physics did little to stimulate students’ interest in the subject, failed to teach them to think like physicists, and afforded few opportunities for them to approach problems in the way that a physicist should. In 1957, after the Soviet Union successfully orbited Sputnik , fear spread in the United States that American schools lagged dangerously behind in science. As one response to the perceived Soviet threat the U.S. government increased National Science Foundation funding in support of PSSC objectives.
The result was a textbook and a host of supplemental materials, including a series of films. In a discussion I was reading on the Phys-L mailing list recently, the PSSC course was discussed and my attention was drawn to two PSSC films that are available from the Internet Archive: “Frames of Reference” (1960) and “Magnet Laboratory” (1959). (Use these links if the embedded players below don’t render properly.) Both are very instructive and highly entertaining. Each lasts about 25 minutes.
Let’s look first at the film on magnets; it’s quite a hoot. First, the background: when I was turning into a physicist I knew some people who went to work at the “Francis Bitter National Magnet Lab” (as it was known at the time) at MIT. This was the place for high-field magnet work.
Well, this film is filmed there when it was just Francis Bitter’s magnet lab, and we’re given demonstrations by Bitter himself, along with a colleague, not to mention a tech who runs a huge electrical generation and is called either “Beans” or “Beams”–I couldn’t quite make it out. These guys have a lot of fun doing their demonstrations.
At one point in the film we hear the phone ringing. Beans calls out: “EB [?], you’re wanted on the telephone.” Bitter replies, without losing the momentum on his current demonstration, “Well, tell ‘em to call me back later, I’m busy.” Evidently multiple takes were not in the plan.
This is great stuff for people who like big machinery and big electricity and big magnets. Watch copper rods smoke while they put an incredible 5,000 amps of current through them. I laughed when Bitter started a demonstration: “All right, Beans, let’s have a little juice here. Let’s start gently. Let’s have about a thousand amps to begin with.” Watch as they melt and then almost ignite one of their experiments. It evidently happened often enough, because they have a fire extinguisher handy.
This next film on “Frames of Reference” is a little less dramatic, but the presenters perform some lovely simple but clever and illustrative experiments, demonstrations that would almost certainly be done today with computer animations so it’s wonderful to see them done with real physical objects. After they make clear what inertial frames of reference are they take a look at non-inertial frames and really clarify some issues about the fictitious “centrifugal force” that appears in rotating frames.
———-
* The photograph comes from the collection of the James Clerk Maxwell foundation.
† Duh.
May
21
Posted by jns on
May 21, 2009
 These are Les Frères Tissandier,* the brothers Albert Tissandier (1839-1906) on the left, and Gaston Tissandier (1843-1899). Albert was the artist, known as an illustrator, and Gaston was the scientist and aviator.†
These are Les Frères Tissandier,* the brothers Albert Tissandier (1839-1906) on the left, and Gaston Tissandier (1843-1899). Albert was the artist, known as an illustrator, and Gaston was the scientist and aviator.†
The Tissandier Brothers were pioneering adventurers (only Gaston did the flying) in high-altitude balloon ascensions. From the U.S. Centennial of Flight Commission’s “The Race to the Stratosphere“:
During the nineteenth century, balloonists had blazed a trail into the upper air, sometimes with tragic results. In 1862 Henry Coxwell and James Glaisher almost died at 30,000 feet (9,144 meters). Sivel and Croc.-Spinelli, who ascended in the balloon Zénith in April 1875 with balloonist Gaston Tissandier, died from oxygen deprivation. The last men of the era of the nineteenth century to dare altitudes over 30,000 feet (9,144 meters) were Herr Berson and Professor Süring of the Prussian Meteorological Institute, who ascended to 35,500 feet (10,820 meters) in 1901, a record that stood until 1931.
The first men to reach 30,000 feet (9,144 meters) did not know what they were facing. It is now known that at an altitude of only 10,000 feet (3,048 meters), the brain loses 10 percent of the oxygen it needs and judgment begins to falter. At 18,000 feet (5,486 feet), there is a 30 percent decrease in oxygen to the brain, and a person can lose consciousness in 30 minutes. At 30,000 feet (9,144 meters), loss of consciousness occurs in less than a minute without extra oxygen.
About that harrowing experience, here is Gaston’s account from his autobiography: Histoire de mes ascensions: recit de vingt-quatre voyage aériens (1868-1877).‡
I now come to the fateful moments when we were overcome by the terrible action of reduced pressure (lack of oxygen). At 22,900 feet torpor had seized me. I wrote nevertheless, though I have no clear recollection of writing. We are rising. Croce is panting. Sivel shuts his eyes. Croce also shuts his eyes. At 24,600 feet the condition of torpor that overcomes one is extraordinary. Body and mind become feebler. There is no suffering. On the contrary one feels an inward joy. There is no thought of the dangerous position; one rises and is glad to be rising. I soon felt myself so weak that I could not even turn my head to look at my companions. I wished to call out that we were now at 26,000, but my tongue was paralyzed. All at once I shut my eyes and fell down powerless and lost all further memory.
He lost consciousness and their balloon ultimately descended while he was unconscious. When he awoke it was to find his two companions dead.
Gaston wrote quite a number of books, over 17 according to his Wikipedia entry. The majority are about ballooning, but it seems that he also had a passion for photography, which was then in its infancy. In fact, several of his titles appear to be in print, including A History and Handbook of Photography.
From Project Gutenberg, two books by Gaston Tissandier are available:
- En ballon! Pendant le siege de Paris (link)
- La Navigation Aérienne L’aviation Et La Direction Des Aérostats Dans Les Temps Anciens Et Modernes (link)
For photographic entertainment, visit this site at the Library of Congress Tissandier Collection of 975 photographs, etchings, and other images emphasizing the early history of ballooning in France; about half of the images are digitized and online.
Finally, because I love research librarians, here is the Library of Congress’ Tracer Bullet on “Balloons and Airships“.
———-
* Crédit photo: Ministère de la Culture (France), Médiathèque de l’architecture et du patrimoine (archives photographiques) diffusion RMN / Référence: APNADAR022912 / Photograph by the studio of Nadar / source link.
† You may have detected the buoyant-flight theme that has preoccupied BoW for a couple of weeks. It’s because I recently read the very enjoyable Lighter than Air : An Illustrated History of Balloons and Airships, by Tom D. Crouch (Baltimore : Johns Hopkins University Press, in association with the Smithsonian National Air and Space Museum, 2009; 191 pages). My book note is here.
‡ From Indiana University’s Lilly Library, an online exhibit called “Conquest of the Skies: A History of Ballooning“, provides a chance to see images from Gaston Tissandier’s book Histoire de mes ascensions: recit de vingt-quatre voyage aériens (1868-1877) (“History of my [balloon] ascensions : accounts of 24 aerial trips”).
May
12
Posted by jns on
May 12, 2009
 This is Ludwig Dürr (1878–1955), remembered as the chief engineer who built the successful Zeppelin airships.
This is Ludwig Dürr (1878–1955), remembered as the chief engineer who built the successful Zeppelin airships.
After an unsatisfactory one-year period in the navy, Dürr was hired, on 15 January 1899, as an engineer at Luftschiffbau Zeppelin GmbH, the company that had been formed by Count Ferdinand Graf von Zeppelin to build rigid, hydrogen-filled airships. While working at their design offices in Stuttgart he completed his last semester of the Royal School of Mechanical Engineering, took his final exams, then Immediately went back to work for Count Zeppelin, moving to the company’s new location in Friedrichshafen, in southwest Germany on the north shore of Lake Constance (“Bodensee” ).
Zeppelin’s company, in the beginning, was beset with difficulties raising money and avoiding disaster. The first dirigible, known as LZ 1 (LZ = “Luftschiff Zeppelin” or “Zeppelin Airship”), at 420 feet long and 32.8 feet in diameter (the largest thing ever built to fly at that time), the airship proved underpowered and hard to manage in strong winds. Bad publicity meant no hoped-for government funding. LZ 1 was broken up for scrap and the company dissolved.
However, Zeppelin kept Dürr around. A few years later King Karl of Württemberg lent his support and Zeppelin, with Dürr as his chief engineer, set out to build LZ 2. This new ship was the same size as LZ 1 but had more power engines (provided by Daimler, as before). It was launched in January1906 from its floating hanger on Lake Constance, as seen in this photograph.

Unfortunately, LZ 2 was also difficult to maneuver in strong winds, but Zeppelin and his crew managed an emergency landing when an engine failed. While they celebrated their safe landing, LZ 2 was destroyed by a storm.
LZ 3, launched that October, flew several flights successfully, but the government wasn’t terribly impressed yet. They gave him money to continue some work, promising to buy LZ3 and LZ 4, provided the latter could stay in the air for 24 hours.
In August 1908 the new airship was taken for a flight up the Rhine Valley. Again, engine failure forced the dirigible down. A storm came along, blew the nose of the ship into a stand of trees, and a hole tore in the gas bags. Rubberized material, flapping the wind, generated a spark that ignited escaping hydrogen and LZ 4 went up in flames.
Now the indefatigable Zeppelin finally felt like the time had come to give up. But then, what happened?
Prepared at last to accept defeat, the seventy-year old Count was stunned by the public outpouring of support that would be remembered as “the miracle of Echterdingen.” Almost without his noticing it, the Count, who had persevered in the face of overwhelming disappointments, emerged as a revered public figure. The old man and his airships decorated a wide range of consumer items, from children’s candies to ladies’ purses, hair brushes, cigarettes and jewelry cases. Copies of the soft white yachting cap that was the Count’s sartorial trademark were sold in stores across Germany, along with an assortment of items from toys to harmonicas bearing Zeppelin’s image. Schools, streets and town squares were renamed in his honor. And now, in his time of greatest need, the German people came to the support of the Count.
In an age of rampant nationalism, Germans looked to the Zeppelin airship as a symbol of national pride. From the Kaiser to the youngest schoolchild, Germans dispatched money to the Count, the sum eventually reaching 6.25 million marks. Those who could not afford to make a cash contribution sent farm products, home-made clothing, anything they thought might help. The ill-fated flight of LZ 4 up the Rhine, Zeppelin would later remark, had been his “luckiest unlucky trip”.
[Tom D. Crouch, Lighter Than Air: An Illustrated History of Balloons and Airships (Baltimore : The Johns Hopkins University Press, 2009), p. 83.]
Zeppelin reformed his company, still with the loyal Dürr as chief engineer, and this time success was theirs and Zeppelin’s name is etched in popular history.
Dürr’s name is not quite so well known as Zeppelin’s, but he’s not forgotten. I was delighted to discover that there is a school in Friedrichshafen named in his honor — the Ludwig-Dürr-Schule — where they are justifiably quite proud of their namesake. Here is the google translation of the page “How has our school its name?” that I’ve enjoyed reading. Visit the welcome page and you can also see the staff plus the menus for lunch.
On the subject of zeppelins, here is a nice, short history by the US Centennial of Flight commission.
There is a Zeppelin Museum in Friedrichshafen. Among many interesting exhibits there is a reconstruction of the passenger areas of the LZ 129 Hindenburg, which famously burst into flames and crashed during landing in Lakehurst, New Jersey on 6 May 1937, killing 35 of the 97 passengers and crewmen aboard. The tragedy brought an end to the practice of filling lighter-than-air ships with highly flammable hydrogen.
Luftschiffbau Zeppelin GmbH is now known as Zeppelin Luftschifftechnik GmbH (in English), and they still build zeppelins. I read that, in conjunction with Airship Ventures, Inc., one of their new zeppelins is making commercial, mostly sightseeing, flights near San Francisco.
Finally, some visual dessert.
Apr
02
Posted by jns on
April 2, 2009
 This is physicist and science-fiction author Gregory Benford. His official website, source of the photograph, tells us that
This is physicist and science-fiction author Gregory Benford. His official website, source of the photograph, tells us that
Benford [born in Mobile, Alabama, on January 30, 1941] is a professor of physics at the University of California, Irvine, where he has been a faculty member since 1971. Benford conducts research in plasma turbulence theory and experiment, and in astrophysics.
Around 1990, the last time I was on a sci-fi binge, I read a number of his books; I see from the official list of novels that I’m behind by a number of books. I should pick up where I left off. I remember Benford’s writing as being very satisfactory from both a science viewpoint and from a fiction viewpoint, although I find that, in my mind, I confuse some of the story-memory details with plots by the late physicist and sci-fi author Charles Sheffield, to whom I give the edge in my preference for hard-science-fiction and adventuresome plots.
But, as is not unprecedented in this forum, Mr. Benford is really providing a pretext–a worthwhile pretext on several counts, clearly, but a pretext nonetheless, because I wanted to talk about “Benford’s Law” and that Benford did not wear a beard.
Frank Benford (1883-1948) was a physicist, or perhaps an electrical engineer–or perhaps both; sources differ but the distinctions weren’t so great in those days. His name is attached to Benford’s Law not because he was the first to notice the peculiar mathematical phenomenon but because he was better at drawing attention to it.
I like this quick summary of the history (Kevin Maney, “Baffled by math? Wait ’til I tell you about Benford’s Law“, USAToday, c. 2000)
The first inkling of this was discovered in 1881 by astronomer Simon Newcomb. He’d been looking up numbers in an old book of logarithms and noticed that the pages that began with one and two were far more tattered than the pages for eight and nine. He published an article, but because he couldn’t prove or explain his observation, it was considered a mathematical fluke. In 1963, Frank Benford, a physicist at General Electric, ran across the same phenomenon, tried it out on 20,229 different sets of data (baseball statistics, numbers in newspaper stories and so on) and found it always worked.
It’s not a terribly difficult idea, but it’s a little difficult to pin down exactly what Benford’s Law applies to. Let’s start with this tidy description (from Malcolm W. Browne, “Following Benford’s Law, or Looking Out for No. 1“, New York Times, 4 August 1998):
Intuitively, most people assume that in a string of numbers sampled randomly from some body of data, the first non-zero digit could be any number from 1 through 9. All nine numbers would be regarded as equally probable.
But, as Dr. Benford discovered, in a huge assortment of number sequences — random samples from a day’s stock quotations, a tournament’s tennis scores, the numbers on the front page of The New York Times, the populations of towns, electricity bills in the Solomon Islands, the molecular weights of compounds the half-lives of radioactive atoms and much more — this is not so.
Given a string of at least four numbers sampled from one or more of these sets of data, the chance that the first digit will be 1 is not one in nine, as many people would imagine; according to Benford’s Law, it is 30.1 percent, or nearly one in three. The chance that the first number in the string will be 2 is only 17.6 percent, and the probabilities that successive numbers will be the first digit decline smoothly up to 9, which has only a 4.6 percent chance.
Take a long series of numbers drawn from certain broad sets, and look at the first digit of each number. The frequency of occurrence of the numerals 1 through 9 are not uniform, but distributed according to Benford’s Law. Look at this figure that accompanies the Times article:
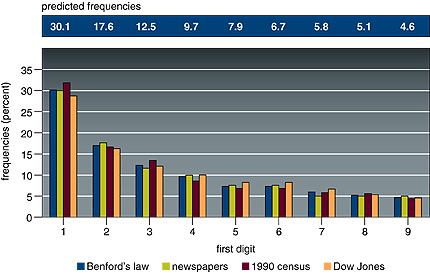
Here is the original caption:
(From “The First-Digit Phenomenon” by T. P. Hill, American Scientist, July-August 1998)
Benford’s law predicts a decreasing frequency of first digits, from 1 through 9. Every entry in data sets developed by Benford for numbers appearing on the front pages of newspapers, by Mark Nigrini of 3,141 county populations in the 1990 U.S. Census and by Eduardo Ley of the Dow Jones Industrial Average from 1990-93 follows Benford’s law within 2 percent.
Notice particularly the sets of numbers that were examined for the graph above: numbers from newspapers (not sports scores or anything sensible, just all the numbers from their front pages), census data, Dow Jones averages. These collections of numbers do have some common characteristics but it’s a little hard to pin down with precision and clarity.
Wolfram Math (which shows a lovely version of Benford’s original example data set halfway down this page) says that “Benford’s law applies to data that are not dimensionless, so the numerical values of the data depend on the units”, which seems broadly true but, curiously, is not true of the original example of logarithm tables. (But they may be the fortuitous exception, having to do with their logarithmic nature.)
Wikipedia finds that a sensible explanation can be tied to the idea of broad distributions of numbers, a distribution that covers orders of magnitude so that logarithmic comparisons come into play. Plausible but not terribly quantitative.
This explanation (James Fallows, “Why didn’t I know this before? (Math dept: Benford’s law)“, The Atlantic, 21 November 2008) serves almost as well as any without going into technical details:
It turns out that if you list the population of cities, the length of rivers, the area of states or counties, the sales figures for stores, the items on your credit card statement, the figures you find in an issue of the Atlantic, the voting results from local precincts, etc, nearly one third of all the numbers will start with 1, and nearly half will start with either 1 or 2. (To be specific, 30% will start with 1, and 18% with 2.) Not even one twentieth of the numbers will begin with 9.
This doesn’t apply to numbers that are chosen to fit a specific range — sales prices, for instance, which might be $49.99 or $99.95 — nor numbers specifically designed to be random in their origin, like winning lottery or Powerball figures or computer-generated random sums. But it applies to so many other sets of data that it turns out to be a useful test for whether reported data is legitimate or faked.
Here’s yet another graph of first digits from vastly differing sets numbers following Benford’s Law (from Lisa Zyga, “Numbers follow a surprising law of digits, and scientists can’t explain why“, physorg.com, 10 May 2007); again one should note the extreme heterogeneity of the number sets (they give “lottery” results to show that, as one truly wants, the digits are actually random):
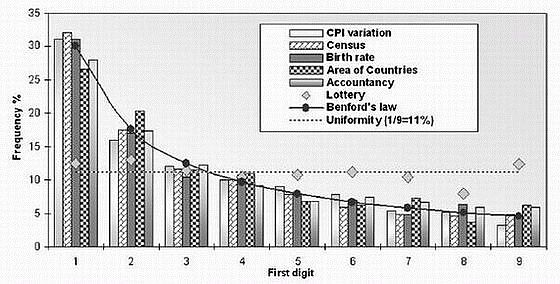
The T.P. Hill mentioned above (in the caption to the first figure), is a professor of mathematics at Georgia Tech who’s been able to prove some rigorous results about Benford’s Law. From that institution, this profile of Hill (with an entertaining photograph of the mathematician and some students) gives some useful information:
Many mathematicians had tackled Benford’s Law over the years, but a solid probability proof remained elusive. In 1961, Rutgers University Professor Roger Pinkham observed that the law is scale-invariant – it doesn’t matter if stock market prices are changed from dollars to pesos, the distribution pattern of significant digits remains the same.
In 1994, Hill discovered Benford’s Law is also independent of base – the law holds true for base 2 or base 7. Yet scale- and base-invariance still didn’t explain why the rule manifested itself in real life. Hill went back to the drawing board. After poring through Benford’s research again, it clicked: The mixture of data was the key. Random samples from randomly selected different distributions will always converge to Benford’s Law. For example, stock prices may seem to be a single distribution, but their value actually stems from many measurements – CEO salaries, the cost of raw materials and labor, even advertising campaigns – so they follow Benford’s Law in the long run. [My bold]
So the key seems to be lots of random samples from several different distributions that are also randomly selected: randomly selected samples from randomly selected populations. Whew, lots of randomness and stuff. Also included is the idea of “scale invariance”: Benford’s Law shows up in certain cases regardless of the units used to measure a property–that’s the “scale” invariance–which implies certain mathematical properties that lead to this behavior with the logarithmic taste to it.
Another interesting aspect of Benford’s Law is that it has found some applications in detecting fraud, particularly financial fraud. Some interesting cases are recounted in this surprisingly (for me) interesting article: Mark J. Nigrini, “I’ve Got Your Number“, Journal of Accountancy, May 1999. The use of Benford’s Law in uncovering accounting fraud has evidently penetrated deeply enough into the consciousness for us to be told: “Bernie vs Benford’s Law: Madoff Wasn’t That Dumb” (Infectious Greed, by Paul Kedrosky).
And just to demonstrate that mathematical fun can be found most anywhere, here is Mike Solomon (his blog) with some entertainment: “Demonstrating Benford’s Law with Google“.
Feb
09
Posted by jns on
February 9, 2009
 This is birthday boy Charles Robert Darwin (1809-1882), born 200 years ago on 12 February 1809. This photograph (which I have cropped) was taken in 1882 by the photographic company of Ernest Edwards, London.*
This is birthday boy Charles Robert Darwin (1809-1882), born 200 years ago on 12 February 1809. This photograph (which I have cropped) was taken in 1882 by the photographic company of Ernest Edwards, London.*
Many people call Darwin’s great idea, common descent through evolution by means of natural selection, the greatest scientific discovery ever. Maybe. It’s certainly big. My hesitation is merely a reflection of my feeling that it’s really difficult to prioritize the great ideas and discoveries of science and math into a hierarchy that would assign the top position to one idea alone. No doubt it’s the over cautious precision of my inner scientist asserting itself.
Almost since the pages of Origin of Species were first sewn into a book there has been a cottage industry of trying to “disprove Darwin”. So strongly associated is his name with the big idea that “Darwin” and “Darwinism” serve as effigies for those who revile the idea so much that they expend considerable energy looking for anything that might weaken the authority of the idea so that it can be toppled from its scientific pantheon.
Unfortunately for their efforts, they sorely misunderstand how science works and, therefore, how futile their efforts are. Detractors seem to believe they are operating under junior debating-society rules where locating any hint of a logical inconsistency in the “theory”, or any modern deviation from what they think is Darwinian orthodoxy, is certain to be a fatal blow to the hated “theory”. Alas, they hope to disprove Darwin but can only disapprove and look silly and naive.
The biggest impediment to tearing down the edifice of “Darwinism”, of course, is reality. Scientists believe that reality has a separate, objective existence that affords no special place to humans. One corollary to this is that objective reality is what it is regardless of our most fervent desires, regardless of our prayers to a supernatural deity to change it, regardless of the stories we tell ourselves over and over about how we would like it to be. Deny reality for your own psychological benefit as needs must, but you will not alter reality by doing so.†
But, suppose there are chinks in the armor of “Darwinism”–isn’t that fatal? Well, no. Great ideas that flow into the vast river of science stay if they are useful ideas. Depending on utility they may change, grow, even evolve over time, but they’re frequently treated as the same idea. Creators do not have veto power over how their scientific ideas are used, nor how they are changed or updated, although they continue to get the credit for great ideas. The way we understand and describe gravity is nothing recognizable to Newton, but he continues to get credit as the discoverer of “universal gravitation”.
But aren’t wrong theories, those that have been “disproven” by logical errors or deviations from precise descriptions of reality, immediately discarded as useless? Oh no, far from it. See the aforementioned Newtonian theory of gravity for but one ready example.‡
This is the trade-off: a somewhat inaccurate (or “wrong”) but productive theory is of far more use to science than a correct but sterile idea. By “productive” I refer to ideas that lead one to new ideas, new experiments, and new understandings. Compare that notion with what some would have you believe is the undeniable perfection of revealed truth from a divine creator: it is an investigative dead end, it leads to no new ideas whatsoever, it affords no solution beyond the parental disclaimer, “because”.
 “Why” is the path science follows, not “because”. I believe that “why” is the more interesting and the more valuable path to follow, at least when it comes to understanding how the universe works. One may feel free to disagree on its value and utility, of course, but denying its reality is futile.
“Why” is the path science follows, not “because”. I believe that “why” is the more interesting and the more valuable path to follow, at least when it comes to understanding how the universe works. One may feel free to disagree on its value and utility, of course, but denying its reality is futile.
———-
* The photograph is part of the wonderful collection of “Portraits of Scientists and Inventors” from the Smithsonian Institution, which we have sampled here before and undoubtedly will again and again, photographs they have contributed to the Flickr Commons Project. (The Flickr page; the persistent URL)
† This is probably the source of the calm, know-it-all demeanor that atheists tend to exhibit, and that so inflames those who would consign us prematurely to the flames of hell: all the evidence we see about how the world really operates fails to suggest that a creator-deity exists–not to mention a personal-coach-deity–and no amount of wishful thinking can change reality.
‡ Sometime we’ll talk about the contingent nature of scientific “truth” and how uncomfortable that idea is for those with an absolutist predilection.
Jan
19
Posted by jns on
January 19, 2009
 This is Sir William Thomson, Baron Kelvin* (1824 – 1907) or, simply, Lord Kelvin as he’s known to us in the physical sciences. This is the same “Kelvin” as in the SI unit “Kelvins”, the degrees of the absolute thermodynamic temperature scale.
This is Sir William Thomson, Baron Kelvin* (1824 – 1907) or, simply, Lord Kelvin as he’s known to us in the physical sciences. This is the same “Kelvin” as in the SI unit “Kelvins”, the degrees of the absolute thermodynamic temperature scale.
The photograph was taken c. 1900 by T. & R. Annan & Sons. I love the title given the photograph by the National Galleries of Scotland: “Sir William Thomson, Baron Kelvin, 1824 – 1907. Scientist, resting on a binnacle and holding a marine azimuth mirror”.
A binnacle, Wikipedia tells me, is a box on the deck of a ship that holds navigational instruments ready for easy reference. One reason Kelvin might be leaning on one is suggested by this bit from the article on “binnacle”
In 1854 a new type of binnacle was patented by John Gray of Liverpool which directly incorporated adjustable correcting magnets on screws or rack and pinions. This was improved again when Lord Kelvin patented in the 1880s another system of compass and which incorporated two compensating magnets.
Kelvin also patented the “marine azimuth mirror” (see the description of “azimuth mirror” from the collection of the Smithsonian National Museum of American History), so the photograph has narrative intent. It seems that Kelvin was an active and successful inventor.
I like this understated biography of Kelvin from the National Galleries of Scotland website (link in first footnote), where it accompanies the photograph:
A child prodigy, William Thomson went to university at the age of eleven. At twenty-two he was appointed Professor of Natural Philosophy in Glasgow where he set up the first physics laboratory in Great Britain and proved an inspiring teacher. He primarily researched thermodynamics and electricity. On the practical side he was involved in the laying of the Atlantic telegraph cable. He was also the partner of a Glasgow firm that made measuring instruments from his own patents.
“He primarily researched thermodynamics and electricity” is a bit of an understatement! Around the time this photograph was taken (c. 1900), Kelvin was pretty much the scientific authority in the world, the great voice of science, the scientist whose opinion on every matter scientific was virtually unassailable.
That unassailability was a huge problem for (at least) Charles Darwin and his theory of common descent by means of natural selection. The crux of the problem was the answer to this question: how old is the Earth?
These days we are quite accustomed to the idea that the Earth is around 4.5 billion years old. At the beginning of the 19th century is was very commonly believed that the Earth was only several thousand years old: Bishop Usher’s calculated date of creation, 23 October 4004 BC, was seen at the time as a scholarly refinement of what everyone already pretty much knew to be true.
Perhaps the big idea growth during the 1800s was the dawning realization of the great antiquity of the Earth. This was accompanied by the realization that fossils might actually be animal remains of some sort; the emergence of geology as a science; and the concept of “uniformitarianism” (an interesting article on the topic), so central to geology, that geological processes in the past, even the deep past, were probably very much like geological processes in action today, so that the geological history of the Earth–and of fossil remains!–could be made sense of.†
Throughout the 19th century discovery after discovery seemed to demand an ever-older Earth. I can imagine that an element of the scientific zeitgeist that precipitated Darwin’s ideas on natural selection as a mechanism for evolution was this growing realization that the Earth might be very, very, very old and that something so remarkably slow as he knew natural selection would be, might be possible. In fact, his ideas went further out on the intellectual limb: he realized that it was necessary that the Earth be much, much older than was currently thought.
In fact, he staked his reputation on the great antiquity of the Earth. This was the critical prediction of his theory, really: the Earth must be vastly older than people thought at the time or else his theory of common descent by natural selection was wrong. It was a bold, seemingly foolhardy claim that he seemed certain to lose.
He was right, of course, but things looked grim at the time and his reasoning was not vindicated by physics until well after his death.
The biggest roadblock to widespread acceptance of the idea of an Earth old enough to allow evolution of humankind through natural selection was none other than Lord Kelvin.
Calculating the age of the Earth looked at the time to be a very challenging problem. But, if there was one thing Kelvin knew, it was that the Earth could not be older than the Sun, and he believed he could calculate the age of the Sun. He was the master of physics, particularly thermodynamics, so all he had to do was add up the sources of energy that contributed to the energy we saw coming from the Sun and figure out how long it might have been going on.
But what were the sources of the Sun’s heat? Kelvin quickly concluded that it could not be any sort of chemical burning, like coal in a fireplace. There simply could not be enough coal. To keep this long story short, Kelvin finally settled on two leading possibilities. One was the energy that came from gravitation contraction of the primordial matter that formed the sun, in which case the sun heated up a great deal originally and then spent eons radiating away its heat. The other possibility that might contribute was the gravitational energy of meteors falling into the sun. (Here’s an interesting and brief exposition of the arguments: S. Gavin, J. Conn, and S. P. Karrer, “The Age of the Sun: Kelvin vs. Darwin“.)
Kelvin published his thoughts in an interesting, and very readable paper, called “On the Age of the Sun’s Heat” , Macmillan’s Magazine, volume 5 (March 5, 1862), pp. 288-293. (html version; pdf version) In the conclusion to that paper Kelvin wrote:
It seems, therefore, on the whole most probable that the sun has not illuminated the earth for 100,000,000 years, and almost certain that he has not done so for 500,000,000 years. As for the future, we may say, with equal certainty, that inhabitants of the earth can not continue to enjoy the light and heat essential to their life for many million years longer unless sources now unknown to us are prepared in the great storehouse of creation.
What an irritant for Darwin! That was not nearly enough time!
These days it is a clichéd joke to say of something that “it violates no known laws of physics”, but that’s the punchline for this entire controversy. Kelvin, naturally, had to search for sources of the Sun’s heat that violated no known laws of physics as they were known at the time, but there were new laws of physics lurking in the wings.
Darwin published On the Origin of Species in 1859. Kelvin published his paper in 1862. Radioactivity was only discovered by Henri Becquerel in 1896. The radioactive decay of elements was not recognized for some time as a possible source of solar energy, but as understanding advanced it was realized that the transmutation of one element into another through radioactive decay involved a loss of mass–the materials before and after could be weighed.
The next domino fell in 1906, a year before Kelvin’s death, when Einstein published his famous equation, 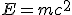 , a consequence of his special theory of relativity. Understanding dawned that the loss of mass was related to a release of energy through the radioactive decay.
, a consequence of his special theory of relativity. Understanding dawned that the loss of mass was related to a release of energy through the radioactive decay.
Our modern knowledge that the sun is powered by nuclear fusion through a process that releases enormous amounts of energy via fusion cycles (interesting, mildly technical paper on its discovery and elucidation) that consume hydrogen atoms to create helium atoms, and then consume those products to produce some heavier elements, was still decades in the future (generally credited to Hans Bethe’s paper published in 1939).
But the message was clear: here was a possible new source of energy for the sun that Kelvin knew nothing about but that could vastly increase the likely age of the Sun.
To finish this part of the story, here is an excerpt from John Gribbin’s The Birth of Time : How Astronomers Measured the Age of the Universe. (New Haven : Yale University Press, 1999. 237 pages.), a fascinating page-turner of a popular science book. (Book note forthcoming.)
If the whole Sun were just slightly radioactive, it could produce the kind of energy that we see emerging from it in the form of heat and light. In 1903, Pierre Curie and his colleague Albert Laborde actually measured the amount of heat released by a gram of radium, and found that it produced enough energy in one hour to raise the temperature of 1.3 grams of water from 0°C to its boiling point. Radium generated enough heat to melt its own weight of ice in an hour–every hour. In July that year, the English astronomer William Wilson pointed out that in that case, if there were just 3.6 grams of radium distributed in each cubic metre of the sun’s volume it would generate enough heat to explain all of the energy being radiated from the Sun’s surface today. It was only later appreciated, as we shall see, that the “enormous energies” referred to by Chamberlin are only unlocked in a tiny region at the heart of the sun, where they produce all of the heat required to sustain the vast bulk of material above them.
The important point, though, is that radioactivity clearly provided a potential source of energy sufficient to explain the energy output of the Sun. In 1903, nobody knew where the energy released by radium (and other radioactive substances) was coming from; but in 1905, another hint at the origin of the energy released in powering both the Sun and radioactive decay came when Albert Einstein published his special theory of relativity, which led to the most famous equation in science, 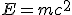 , relating energy and mass (or rather, spelling out that mass is a form of energy.) This is the ultimate source of energy in radioactive decays, where careful measurements of the weights of all the daughter products involved in such processes have now confirmed that the total weight of all the products is always a little less than the weight of the initial radioactive nucleus–the “lost” mass has been converted directly into energy, in line with Einstein’s equation.
, relating energy and mass (or rather, spelling out that mass is a form of energy.) This is the ultimate source of energy in radioactive decays, where careful measurements of the weights of all the daughter products involved in such processes have now confirmed that the total weight of all the products is always a little less than the weight of the initial radioactive nucleus–the “lost” mass has been converted directly into energy, in line with Einstein’s equation.
Even without knowing how a star like the Sun might do the trick of converting mass into energy, you can use Einstein’s equation to calculate how much mass has to be used up in this way every second to keep the Sun shining. Overall, about 5 million tonnes of mass have to be converted into pure energy each second to keep the sun shining. This sounds enormous, and it is, by everyday standards–roughly the equivalent of turning five million large elephants into pure energy every second. But the Sun is so big that it scarcely notices this mass loss. If it has indeed been shining for 4.5 billion years, as the radiometric dating of meteorite samples implies, and if it has been losing mass at this furious rate for all that time, then its overall mass has only diminished by about 4 percent since the Solar System formed.
By 1913, Rutherford was commenting that “at the enormous temperatures of the sun, it appears possible that a process of transformation may take place in ordinary elements analogous to that observed in the well-known radio-elements,” and added, “the time during which the sun may continue to emit heat at the present rate may be much longer than the value computed from ordinary dynamical data [the Kelvin-Helmholtz timescale].” [pp. 36--38]
Kelvin was not always right.
———-
* I’ve taken this image from the Flickr Commons set uploaded by the National Galleries of Scotland, and cropped it some from the original: Source and National Galleries page.
† The history of these ideas in the context of geology as an emerging science is very ably traced in Simon Winchester’s The Map that Changed the World : William Smith and the Birth of Modern Geology (my book note).
Dec
01
Posted by jns on
December 1, 2008
 This beard belongs to Mr. Spock, the venerable half-Vulcan who served as the science officer aboard the Enterprise in “Star Trek”, the original television series. It is thought that he has another name that is unpronounceable by humans. In grade school I identified quite a bit with Mr. Spock. Personally I hoped to develop the cool, rational demeanor and analytical outlook he displayed; outwardly, it was because my ears were too big for my head and looked vaguely pointy.
This beard belongs to Mr. Spock, the venerable half-Vulcan who served as the science officer aboard the Enterprise in “Star Trek”, the original television series. It is thought that he has another name that is unpronounceable by humans. In grade school I identified quite a bit with Mr. Spock. Personally I hoped to develop the cool, rational demeanor and analytical outlook he displayed; outwardly, it was because my ears were too big for my head and looked vaguely pointy.
It seems that this episode in which Spock had this beard (“Mirror, Mirror“), is the only time Spock was ever portrayed with a beard (and, in fact, the bearded version is a mean, anti-Spock in a parallel universe–his beard kept viewers clued in about which universe events were happening). I think that’s too bad because he looks quite dashing in a beard, but apparently NBC already found the Spock character too “sinister” looking to begin with, and everyone knows beards make men look more sinister.
“Spock’s Beard” is also the name of a progressive rock band I’d never heard of until this morning. Isn’t it splendid to learn new things?
Surely, in addition to the main characters, one of the most recognizable things from the “Star Trek” series was the theme song. Last night, for reasons we may or may not get to, the conversation happened to turn on the question whether the familiar and unusual timbre of the melody was 1) a woman singing; or 2) a theremin, which sounded like a woman singing?
Happily, Wikipedia was there with the answer:
Coloratura soprano Loulie Jean Norman imitated the sound and feel of the theremin for the theme for Alexander Courage’s theme for the original Star Trek TV series. Soprano Elin Carlson sang Norman’s part when CBS-Paramount TV remastered the program’s title sequence in 2006.
I was relieved. I had always thought it was a woman singing, but it did sound remarkably like a theremin. And now we’ve arrived at my real object for this piece: Theremin and his theremin. (He never had a beard, it seems, but I would not be thwarted!)
Léon Theremin (1896–1993), born in Russia, started out as Lev Sergeyevich Termen. His name is familiar to many people these days because he invented the “theremin” (here’s an interesting short piece about the theremin; or course there’s Wikipedia on the theremin, not to mention Theremin World). Theremin invented the instrument in 1919 when he was doing research on developing a proximity sensor in Russia. Lenin loved it. Some ten years later Theremin ended up in New York, patented his instrument, and licensed RCA to build them.
The theremin (played by a “thereminist”) is generally deemed to have been the first ever electronic instrument. It also claims the distinction that it is played by the thereminist without being touched. Instead, the thereminist moves her hands near the two antennae of the instrument, one of which controls pitch and the other of which controls volume; capacitive changes between the antennae and the body of the thereminist affect the frequency of oscillators that alter the pitch and volume of the generated tone.
It is a very simple device and the musical sound is not very sophisticated, and yet there’s something beguiling in watching a good thereminist perform, and something haunting about the sound.
Most people have heard a theremin and typically haven’t recognized it. Most popularly, perhaps, is its appearance in the Beach Boys’ “Good Vibrations”, by Brian Wilson (YouTube performance), although this appears to be a modified theremin played by actually touching it!
My favorite theremin parts are in the score Miklós Rózsa wrote for the Hitchcock film “Spellbound“–fabulous film, fabulous music, for which Rózsa won an Academy Award. (In a bit, a link where you can hear the “Spellbound” music, with theremin). This movie was the theremin’s first outing in such a popular venue–”Spellbound” was the mega-hit, big-budget, highly marketed blockbuster of its day. Later on, of course, the theremin was widely used in science-fiction movies, famously The Day the Earth Stood Still and Forbidden Planet. (On the use of the theremin in film scores, here’s a fascinating article by James Wierzbicki: “Weird Vibrations: How the Theremin Gave Musical Voice to Hollywood’s Extraterrestrial ‘Others’ “).
There seems to have been a resurgence of interest in the theremin in the past few years, or else I’ve just noticed other people’s interest more–the internet can make such things much more visible and seemingly more prevalent. One recent development: a solar-powered theremin that fits in an Altoids box. (Heard, by the way, in the radio program mentioned below.)
Some claim that the new interest began following the release of Steven M. Martin’s 1995 documentary, “Theremin: An Electronic Odyssey“. I don’t know about that, but we did watch this film a few weeks ago (we got a copy for rather few dollars–we couldn’t pass it up because of the rather lurid cover art more suitable for something like “Plan Leon from Outer Space” perhaps), and it is an outstanding documentary. It’s about Theremin and the theremin, and the story is very, very engaging. There’s a lot of weird stuff that went on in Theremin’s very long life, like the time in the 1930s (I think) when he was snatched from his office in New York City by Russian agents and spirited away to the Soviet Union. Friends thought he was dead, but he reappeared years later. He’d been forced to work for the KGB developing small listening devices.
A few people of interest also show up in the film: Brian Wilson (enjoy watching him try to finish one thought or get to the end of a sentence), Nicolas Slonimsky, Todd Rundergren, Clara Rockmore, and Robert Moog (of the Moog Synthesize–he started out making theremin kits). Of particular interest, I thought, was Clara Rockmore (1911–1998), thought of as probably the greatest thereminist of all time. Listening to her talk in the film is interesting, but more interesting is watching and listening to her play the theremin. Check out her technique! It’s great stuff.
Now for one last treat. Here is a link to a 90-minute radio program (and information about it), called “Into the Ether“, presented by a British thereminist who performs under the name “Hypnotique”. The program is nicely done and filled with audio samples of theremin performances in a wide variety of genres. If you don’t have the time for the entire thing, I’ll point out that the “Spellbound Concerto”, by Miklós Rózsa, from his music for the film, is excerpted at the very beginning of the program and that’s a must-hear for thereminophiles, whether new or seasoned.
Aug
18
Posted by jns on
August 18, 2008
 This is British physicist James Prescott Joule (1818-1889), the same Joule who gave his name (posthumously) to the SI unit for energy. Wikipedia’s article on Joule and his most noted contribution to physics is admirably succinct:
This is British physicist James Prescott Joule (1818-1889), the same Joule who gave his name (posthumously) to the SI unit for energy. Wikipedia’s article on Joule and his most noted contribution to physics is admirably succinct:
Joule studied the nature of heat, and discovered its relationship to mechanical work (see energy). This led to the theory of conservation of energy, which led to the development of the first law of thermodynamics.
At the time that Joule was doing his work, heat was still thought to be caused by the presence of the substance “caloric”: when caloric flowed, heat flowed. That idea was coming under strain thanks largely to new experiments with electricity and motors and observations that electricity passing through conductors caused the conductors to heat up, a notion that proved incompatible with the theory of caloric. This was also still early days in the development of thermodynamics and ideas about heat, work, energy, and entropy had not yet settled down into canon law.
Joule found that there was a relationship between mechanical work (in essence, moving things around takes work) and heat, and then he measured how much work made how much heat, a key scientific step. His experiment was conceptually quite simple: a paddle in a bucket of water was made to turn thanks to a weight falling under the influence of gravity from a fixed height. As a result the water heated up a tiny bit. Measure the increase in temperature of the water (with a thermometer) and relate it to the work done by gravity on the weight (calculated by knowing the initial height of the weight above the floor).
In practice, not surprisingly, it was a very challenging experiment.* The temperature increase was not large, so to measure it accurately took great care, and Joule needed to isolate the water from temperature changes surrounding the water container, which needed insulation. Practical problems abounded but Joule worked out the difficulties over several years and created a beautiful demonstration experiment. He reported his final results in Cambridge, at a meeting of the British Association, in 1845.
Joule’s experiment is one of the ten discussed at some length in George Johnson, The Ten Most Beautiful Experiments (New York : Alfred A. Knopf, 2008, 192 pages), a book I recently finished reading and which I wrote about in this book note. It was a nice book, very digestible, not too technical, meant to present some interesting and influential ideas to a general audience, ideas that got their shape in experiments. Taken together the 10 essays also give some notion of what “beauty” in a scientific experiment might mean; it’s a notion intuitively understood by working scientists but probably unfamiliar to most nonscientists.
__________
* You knew that would be the case because people typically don’t get major SI units named after them for having done simple experiments.
Aug
11
Posted by jns on
August 11, 2008

This is Georg Cantor (1845–1918), the German mathematician who advanced set theory into the infinite with his discovery/invention of transfinite arithmetic. Why I hedge over “discovery” or “invention” we’ll get to in a moment.
I first encountered Cantor’s ideas in college in my course of “mathematical analysis”, which was largely concerned with number theory. I remember the stuff we worked on as beautiful but nearly inscrutable, and very dense: our textbook was less than an inch thick but the pages were dark with mathematical symbols, abbreviations, and shorthand, so that a semester was much too short a time to get through the whole thing.
Cantor proved a series of amazing things. First, consider the positive integers (or natural numbers, or whole numbers, or counting numbers): 1, 2, 3, 4, etc. We know that there is no largest integer because, if there were, we could add 1 to it to get one larger. Therefore, the set of positive whole numbers is infinite. This is also described as a countable, or denumerable infinity, because the elements of the set can be put into a one-to-one correspondence with the counting numbers–a rather obvious result because they are the counting numbers and can thus be counted. Think of counting and one-to-one correspondence for a bit and is becomes obvious (as the textbooks are wont to say) that the set of positive and negative integers (…,-3, -2, -1, 0, 1, 2, 3, …) is also a countable infinity, i.e., there are just as many positive and negative integers as there are positive ones. (This is transfinite arithmetic we’re talking about here, so stay alert.)
Next to consider is the infinity of rational numbers, or those numbers that can be written as the ratio of two whole numbers, i.e., fractions. How infinite are they compared to the whole numbers?
Cantor proved that the cardinality of the rational numbers is the same as that of the whole numbers, that the rational numbers are also denumerable. For his proof he constructed a system of one-to-one correspondence between the whole numbers and the rationals by showing how all of the rational numbers (fractions) could be put into an order and, hence, counted. (The illustration at the top of this page shows how the rationals can be ordered without leaving any out.)
Any set whose elements can be put into a one-to-one correspondence with the whole numbers, i.e., that can be counted, contains a countable infinity of elements. Cantor gave a symbol to this size, or cardinality, or infinity, calling it 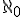 (said “aleph nought”), using the first letter of the Hebrew alphabet, named “aleph”.
(said “aleph nought”), using the first letter of the Hebrew alphabet, named “aleph”.
Then there are the irrational numbers, numbers that cannot be written as ratios of whole numbers. The square root of 2 is a famous example; discovery of its irrationality is said to have caused great consternation among Pythagoreans in ancient times. There are several interesting classes of irrational numbers, but for this consideration it is enough to say that irrational numbers have decimal expansions that never terminate and whose digits never repeat.  , the ratio of the circumference to the diameter of a circle is a famous irrational number and many people are fascinated by its never ending decimal representation.
, the ratio of the circumference to the diameter of a circle is a famous irrational number and many people are fascinated by its never ending decimal representation.
Cantor proved that the cardinality of the real numbers (rational and irrationals put together) is greater than 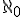 — they cannot be counted. He proved this with his diagonalization technique, in which he showed that no matter how many rational numbers were packed into an interval one more could always be constructed that was not in that set.* (For the proof, see this Wikipedia page; it’s not a difficult proof to read but it takes a clear head to understand it.)
— they cannot be counted. He proved this with his diagonalization technique, in which he showed that no matter how many rational numbers were packed into an interval one more could always be constructed that was not in that set.* (For the proof, see this Wikipedia page; it’s not a difficult proof to read but it takes a clear head to understand it.)
Cantor referred to the real numbers as the continuum because it was so dense with numbers. Cantor had shown that the cardinality of the continuum was strictly larger than the cardinality of the whole numbers. Now we have two sizes of infinity, if you will! There are more, but we’ll stop there.
Cantor was haunted by being unable to prove something he believed to be true, known as the “continuum hypothesis”. In words the conjecture is that there is no cardinality of infinity between the cardinality of the countable infinity and the cardinality of the real numbers. When he’d reached this stage Cantor’s mental health faced severe challenges and he became obsessed with trying to prove that Francis Bacon wrote the plays of Shakespeare. A decade after Cantor died Kurt Gödel proved that the Continuum Hypothesis was a formally undecidable proposition of set theory, that it could neither be proved or disproved.
Much of this story appeared in one book I finished recently: Amir D Aczel, The Mystery of the Aleph : Mathematics, the Kabbalah, and the Search for Infinity (New York : Four Walls Eight Windows, 2000, 258 pages). My book note is here.
Just after that book I finished another book on a mathematical topic: Mario Livio, The Golden Ratio : The Story of Phi, The World’s Most Astonishing Number (New York : Broadway Books, 2002, viii + 294 pages). Its book note is here.
Aside from their interest in mathematical topics, the two books have very little in common with one exception: both authors ruminated on the question whether mathematics is created or discovered, whether the great edifice exists only in the minds of humans or whether it somehow has an independent existence in the universe independent of the human mind. The complication to the question of course is the remarkable utility of mathematics when it comes to explaining how the universe works.
I once had a long-time debate with my roommate in graduate school on the question. I remember winning the debate after months, but I forget which side I argued. It’s the sort of thing that physics and philosophy graduate students argue about.
Oddly to me, aside from the vague coincidence that two books I should read back-to-back considered this question,† is that each author felt very strongly about the answer to the question, feeling that his answer was the obvious best choice, but, as you’ve guessed, one believed that mathematics was obviously discovered and the other felt that mathematics was clearly invented.
Even as I once argued that mathematics was obviously discovered, I realized from reading these two authors’ discussions that I now pretty much would go with the conclusion that mathematics is an invention of the human mind. Now, how that could be and still have mathematics accord so well with the operating of the universe is a question that I’m afraid goes well beyond the scope of this already too long posting.
Besides, the hour grows late and my mind lacks the clarity to be convincing right now. So, as a distraction, I leave you thinking about the much simpler question of how one type of infinity can be larger than another.
__________
* Think very carefully about the distinction between not being able to think of a way to count the set versus proving that there is no way it can be done.
† Not so surprising, really, if you consider the fact that when I’m browsing for books on the library stacks I’ll frequently find more than one on a single shelf that looks interesting.
 This is the youthful Galileo Galilei (1564–1642), who established the intellectual starting point for this short discussion.
This is the youthful Galileo Galilei (1564–1642), who established the intellectual starting point for this short discussion. This* is Scottish physicist James Clerk Maxwell (1831–1879). He did significant work in several fields (including statistical physics and thermodynamics, in which I used to research) but his fame is associated with his electromagnetic theory. Electromagnetism combined the phenomena of electricity and magnetism into one, unified field theory. Unified field theories are still all the rage. It was a monumental achievement, but there was also a hidden bonus in the equations. We’ll get to that.
This* is Scottish physicist James Clerk Maxwell (1831–1879). He did significant work in several fields (including statistical physics and thermodynamics, in which I used to research) but his fame is associated with his electromagnetic theory. Electromagnetism combined the phenomena of electricity and magnetism into one, unified field theory. Unified field theories are still all the rage. It was a monumental achievement, but there was also a hidden bonus in the equations. We’ll get to that.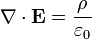
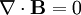
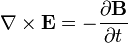
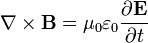
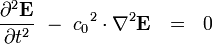
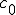 , which is related to the product of the physical constants
, which is related to the product of the physical constants  and
and 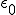 that appeared in the earlier equations.
that appeared in the earlier equations.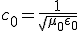
 These are Les Frères Tissandier,* the brothers Albert Tissandier (1839-1906) on the left, and Gaston Tissandier (1843-1899). Albert was the artist, known as an illustrator, and Gaston was the scientist and aviator.†
These are Les Frères Tissandier,* the brothers Albert Tissandier (1839-1906) on the left, and Gaston Tissandier (1843-1899). Albert was the artist, known as an illustrator, and Gaston was the scientist and aviator.† This is Ludwig Dürr (1878–1955), remembered as the chief engineer who built the successful Zeppelin airships.
This is Ludwig Dürr (1878–1955), remembered as the chief engineer who built the successful Zeppelin airships.
 This is physicist and science-fiction author Gregory Benford. His
This is physicist and science-fiction author Gregory Benford. His 

 This is birthday boy Charles Robert Darwin (1809-1882), born 200 years ago on 12 February 1809. This photograph (which I have cropped) was taken in 1882 by the photographic company of Ernest Edwards, London.*
This is birthday boy Charles Robert Darwin (1809-1882), born 200 years ago on 12 February 1809. This photograph (which I have cropped) was taken in 1882 by the photographic company of Ernest Edwards, London.*
 This is Sir William Thomson, Baron Kelvin* (1824 – 1907) or, simply, Lord Kelvin as he’s known to us in the physical sciences. This is the same “Kelvin” as in the SI unit “Kelvins”, the degrees of the absolute thermodynamic temperature scale.
This is Sir William Thomson, Baron Kelvin* (1824 – 1907) or, simply, Lord Kelvin as he’s known to us in the physical sciences. This is the same “Kelvin” as in the SI unit “Kelvins”, the degrees of the absolute thermodynamic temperature scale.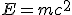 , a consequence of his special theory of relativity. Understanding dawned that the loss of mass was related to a release of energy through the radioactive decay.
, a consequence of his special theory of relativity. Understanding dawned that the loss of mass was related to a release of energy through the radioactive decay. This beard belongs to Mr. Spock, the venerable half-Vulcan who served as the science officer aboard the Enterprise in “Star Trek”, the original television series.
This beard belongs to Mr. Spock, the venerable half-Vulcan who served as the science officer aboard the Enterprise in “Star Trek”, the original television series.  This is British physicist James Prescott Joule (1818-1889), the same Joule who gave his name (posthumously) to the SI unit for energy.
This is British physicist James Prescott Joule (1818-1889), the same Joule who gave his name (posthumously) to the SI unit for energy. 
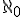 (said “aleph nought”), using the first letter of the Hebrew alphabet, named “aleph”.
(said “aleph nought”), using the first letter of the Hebrew alphabet, named “aleph”. , the ratio of the circumference to the diameter of a circle is a famous irrational number and many people are fascinated by its never ending decimal representation.
, the ratio of the circumference to the diameter of a circle is a famous irrational number and many people are fascinated by its never ending decimal representation.