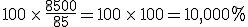On Not Finishing Kaku’s “Physics of the Impossible”

I read a lot of popular-science books. You know I do this partly to support the Science Booknotes and Science Book Challenge projects at Scienticity. I often remark to myself how thoroughly I enjoyed a book that I chose arbitrarily at my library, maybe because the title appealed to me or the book spine was the right color for me that evening. The implication for me, I’m happy to say, is that there is a great deal of really very good writing about science for the non-specialist. It’s satisfying to review these books and let other potential readers know about the great ideas they discuss.

Sometimes, of course, I select a book that turns out not to suit my taste for some reason. Generally speaking I prefer not to review a book I didn’t care for because I don’t see the point of a negative review about a book whose subject matter didn’t really appeal to me or whose author wrote in a style that I found unsympathetic. After all, many others might find the book worthwhile or tune in to that author’s particular style, and I’d much rather have a review in our booknotes collection setting out positive reason why a potential reader might choose to read a particular title.

Then there is the small but difficult category of books that I never finish reading because, for some reason or another, I find them too overwhelmingly irritating. For instance, I never finished reading Stephen Jay Gould’s The Hedgehog, the Fox, and the Magister’s Pox (my booknote) because his writing was so bad, and so badly edited, that I conjectured that it had been written by pod people who had taken over his body. Happily, these are rare events, but sometimes it seems important to write about them.

What to do, then, when I find an author known for his (or her) enthusiastic and entertaining advocacy and popularizing for science whose writing exhibits a notable disregard for precision about scientific facts and, furthermore, who seems to have a superficial or incorrect understanding of parts of his or her subject matter?

When I read a book that I plan to write about, I keep a folded sheet of paper inside the back cover where I make notes of interesting ideas, things to mention, and possible quotations for use in a review. I also make a note of trouble spots in the text: unclear or badly written explanations, confusion over facts of science, and such things. When I have filled the pages with errors the author has made and I’m only on page 30 of the book, I know I have trouble on my hands, and a quandary. I can easily stop reading the book, but I have to decide whether to write about it or not. Is there a useful point — beyond venting my spleen — to writing about bad science writing?

I have such a case on hand with Michio Kaku’s Physics of the Impossible_{*, in which the (apprently) well-known science popularizer talks about the physics and possibility of such science-fiction staples as invisibility cloaks, force fields, time travel, and such topics. It’s a very appealing idea, I thought, but I had to stop reading; there were simply too many errors–some serious errors–of science to continue, all before I reached page 30, less than one-tenth of my way through the book.}

Let’s begin by going through some of the problems that I had in these early pages.

1. Conflating Historic Events

“Growing up, I remember my teacher one day walking up to the map of the Earth on the wall and pointing out the coastlines of South America and Africa. Wasn’t it an odd coincidence, she said, that the two coastlines fit together, almost like a jigsaw puzzle? Some scientists, she said, speculated that perhaps they were once part of the same, vast continent. But that was silly. [...] Later that year we studied the dinosaurs. Wasn’t it strange, our teacher told us, that the dinosaurs dominated the Earth for millions of years, and then one day they all vanished? No one knew why they had all died off. Some paleontologists thought that maybe a meteor from space had killed them, but that was impossible; more in the realm of science fiction [pp. xi--xii]

The idea that the continents might once have fitted together is a very old one, evident to most anyone who ever looked at a world map. These days we have at hand the well-established theory of plate techtonics to explain how it all could have happened, and certainly did happen. In the earlier twentieth century geologists and others began thinking more seriously about the idea of continents moving, but it was experimental results in the late 1950s and early 1960s that finally overthrew “conventional wisdom” that the continents couldn’t just move around. Plate techtonics was well established as scientific orthodoxy by 1965.

The Alvarez Theory, the idea that the extinction of the dinosaurs was brought about by the impact with Earth of a large body from space, was first proposed by Luis and his son Walter Alvarez following on Walter’s discovery of a thin sedimentary layer of iridium that dated closely to the time when dinosaurs disappeared. That theory did not appear until 1980. For many years afterwards the idea that an asteroid impact wiped out the dinosaurs was widely thought preposterous; before that time it hadn’t even been thought of. By now, of course, it’s widely familiar to the general public.

I hope you see my difficulty by now. The author writes that his teacher taught him that 1) some scientists speculated that continents drifted, an assertion that only makes sense prior to 1965, when Plate Techtonics was established; and 2) that some scientists though maybe an asteroid had killed the dinosaurs, an idea that no one had thought of until 1980. He writes that his teacher taught him these things in the same year, even though the closest in actual time that they may have come to each other is 15 years. In other words, this makes a good story but it’s highly unlikely that these two events took place in the same year.

2. Confusing Words and Ideas

This problem is more subtle. In the first chapter Kaku has a section on “force fields”, a common technology of science-fiction worlds for decades. Kaku unfortunately takes the words too literally and conflates the notion of a science-fiction “force field” with some combination of the ideas of “forces” and “fields” as they are used in physics, and so he spends some time talking about the four fundamental forces of the universe (gravitation, electromagnetism, the weak force, and the strong force) and discusses to some extent how each of these is formulated mathematically as “field theories”. But one does not get “force fields” by simply combining these two concepts. He confuses the reader over these pairs of words used differently in two different realms, and then leaves the reader with the mistaken impression that “force fields” might become reality just as soon as physics catches up and discovers a new field theory for a “fifth force”. None of this has anything useful to do with the concept of a “force field” as it’s deployed by science-fiction authors.

3. Casual Writing Leads to Mistaken Readings

In another space I’ll write about what I think should be the prime directive of any writer about science : First, Do Not Mislead. Writing about science for a popular audience is an awesome responsibility; scientifically literate readers can fend for themselves, but if the author has in mind an audience of nonspecialists, it is vital that the author take the utmost care with describing and explaining facts from science, because the nonspecialist reader can easily invent his or her own mistaken notion of how nature works when presented with sloppy, incomplete, or imprecise exposition. I expect popular science writers to

1. Get it right, and
2. Say it clearly.

Here are just some examples of statements that I felt violated the Prime Directive in Kaku’s writing. First, from the section on “Magnetic Levitation”:

“One common property of superconductivity is called the Meissner effect.” [p. 14]

When a superconductor in a magnetic field is cooled from its normal (non-superconducting) phrase to its superconducting phrase, it “expels” the external magnetic field from it’s interior, which is to say that it creates on its surface electrical currents that themselves create a magnetic field that just cancels the externally imposed field within the superconductor. This is known as the “Meissner Effect”, named for Walther Meissner. This is a defining characteristic of superconductors, a property necessarily exhibited by every superconductor. I find it odd to refer to it as a “common property of superconductivity”, as though it’s an incidental property seen in only some, perhaps many, superconductors, but suggesting that it is not a universal property.

In a section on “Invisibility”, discussing the possibility of an “invisibility cloak”:

“But today the impossible may become possible. New advances in “metamaterials” are forcing a major revision of optics textbooks. [p. 17]

Actually, the manufactured metamaterials that Kaku refers to, surprising and ingenious as they are, behave according to well-understood principles, requiring no “revision”, just an increase in understanding how to manufacture materials with desirable optical properties. This is misleading and a type of sensationalism that doesn’t serve the cause of increasing science literacy.

Later in the section on “Invisibility”, Kaku turns to a discussion of electromagnetic fields, namely, James Maxwell’s great advance in physical theory in the 19th century:

“(…If he [Maxwell] had lived longer, he might have discovered that his equations allowed for distortions of space-time that would lead directly to Einstein’s relativity theory. [p. 19]

Now, here is a frequent problem with those who write about science. There are, in fact, two distinct theories of Einstein commonly referred to as “relativity” : the theory of “Special Relativity”, from 1905, and the theory of “General Relativity”, from 1916. Special relativity is a theory of electrodynamics, basically a theory of light, which also introduced the idea of four-dimensional “space-time” and that most famous of equations, E=mc^2. General relativity is a theory of gravitation, a geometrical theory that treats gravity as deformations in space-time.

Usually the context makes clear which “relativity” the author meant. But here our only guide is that Kaku speaks of “distortions of space-time”. In special relativity travel at high velocities bring about time dilations and length contractions (“Lorentz Transformations”), i.e., distortions of space-time. In general relativity, gravitational effects are produced by the distortions of space-time caused by mass.

Carelessness here has caused a confusion that can’t be untangled and therefore does nothing to enlighten the nonspecialist reader who may not distinguish the two “relativity” theories so easily to begin with.

4. Errors of Physical Fact

These were the most troubling errors that confronted me in reading the first sections of Kaku’s book. Troubling because it betrays the trust between the nonspecialist reader and the authoritative voice of the author to make statement of physical fact, or to give descriptions of physical systems, that are imprecise or simply incorrect. I find it even more troubling when the author is a physicist who should be expected to get it right.

Back to the pages of discussion about Maxwell’s Theory of Electrodynamics, the author writes:

Maxwell began with Faraday’s discovery that electric fields could turn into magnetic fields and vice versa. He took Faraday’s depictions of force fields and rewrote them in the precise language of differential equations, producing one of the most important series of equations in modern science. They are a series of eight fierce-looking differential equations. Every physicist and engineer in the world has to sweat over them when mastering electromagnetism in graduate school [p. 18].

While it is certainly true that every physicist and engineer had to sweat over the equations in graduate school–probably even using the same, nearly universally taught textbook–the italicized phrase (my italics) would raise any student’s eyebrows. Whether the equations are “fierce-looking” or not is a matter of taste (I think they’re rather elegantly simple myself), there are in fact only four equations, two for the electric field and two for the magnetic field.

I nearly dropped the book when I read this — I couldn’t imagine how any physicist could have come to refer to “eight” equations. Now, while it’s true that the electric and magnetic fields are written in modified form when they occur in materials, rather than vacuum, the equations stay the same. That there are two each for the electric and magnetic fields is fundamentally characteristic of the entire field theory.

Slightly further on, Kaku offers this analysis of the property of optical transparency in materials:

Maxwell’s theory of light and the atomic theory give simple explanations for optics and invisibility. In a solid, the atoms are tightly packed, while in a liquid or gas the molecules are spaced much farther apart. Most solids are opaque because light rays cannot pass through the dense matrix of atoms in a solid, which act like a brick wall. Many liquids and gases, by contrast, are transparent because light can pass more readily between the large spaces between their atoms, a space that is larger than the wavelength of visible light. For example, water, alcohol, ammonia, acetone, hydrogen peroxide, gasoline, and so forth are all transparent, as are gases such as oxygen, hydrogen, nitrogen, carbon dioxide, methane, and so on.

There are some important exceptions to this rule. Many crystals are both solid and transparent. But the atoms of a crystal are arranged in a precise lattice structure, stacked in regular rows, with regular spacing between them. Hence there are many pathways that a light beam may take through a crystalline lattice. Therefore, although a crystal is as tightly packed as any solid, light can still work its way through the crystal.
Under certain circumstances, a solid object may become transparent if the atoms are arranged randomly [as in a glass]. [pp. 25--26]

It’s at this point that I threw up my metaphorical hands in despair and stopped reading the book. This “explanation” of transparency is so totally wrong I hardly know where to begin.

Light, namely, propagating electromagnetic waves, only interact with matter via the electromagnetic field (with a notable exception in General Relativity that doesn’t impinge on this discussion); in other words, light waves are sensitive to electrical charges, electrical currents, and magnetic fields. They sense the electrical charge of the electron “cloud” around an atomic nucleus; they might sense the positive charge of protons in a nucleus if they can get close enough for it to have an effect. Electromagnetic waves–light waves or photons, pick your favorite representation–do not interact with the mass of matter itself. Whether atoms are heavy or not heavy makes no difference, the light doesn’t sense the mass. Hold that thought.

Now, while it is true that the atoms in a liquid or solid are much closer together than they are in a gas, the atoms are still so physically small and so distantly separated relative to their physical sizes–not to mention that the components of an atom are vastly tinier than the “size” of the atom itself–that most of matter, whether solid, liquid, or gas, is still empty space. Even in a crystal or a glass this is true. Physically, the mass of atoms occupies exceedingly little of the space of the object they make up. By “exceedingly little” I mean this: the volume of the atomic nucleus is only about 1/1,000,000,000,000^th the approximate volume of the atom itself.

I hope it’s becoming clear by this point that how close the atoms are together has relatively little bearing on how much “space” in matter is taken up by substantial parts of the atoms. The simple deduction, then, is that material objects are not more transparent or less transparent because the atoms are closer or further apart such that they “block” the light. The light does not run into the atoms and get blocked by their physical size. They are in no sense like a “brick wall” in any way that I can imagine makes sense.

The transparency of any given substance is determined by the not-so-simple interaction between light waves of particular frequencies (or “colors”) and the electric fields (predominantly) created in the substance by the particular configuration of its atoms. Gases do tend to be relatively transparent because the wide separation of their atoms creates a weakly interacting electric field. Nevertheless, some gasses do have colors because their atoms absorb certain wavelengths of light preferentially, through light waves being absorbed and/or emitted by the atomic electrons. Crystals have complicated and varied optical properties — transparency, opacity, colors in gemstones, birefringence, polarization rotations, etc. — depending sensitively on the periodically varying electric field inside the crystal that is produced by the regular (crystalline) placement of the atoms; but do keep your mind on the electric field inside the crystal, not the atoms “blocking” the light. There are also materials that are mostly opaque to visible light but that can be transparent in wavelengths of light that our eyes do not detect. The optical properties of materials is a rich field with lots of interesting effects and phenomena; get a taste for it, if you like, by looking up “transparency” in Wikipedia.

Looking up “transparency” is apparently something that author Kaku didn’t bother to do when he should have. His explanation of the phenomenon I find so confused and misleading that I feel his writing does a serious disservice to the nonspecialist who reads his book hoping for understanding from a scientist who knows what he’s talking about. This is why I stopped reading the book at this point, and why I have chosen to write about it.

One or two of the objections I noted earlier on amount to very little. I frequently find one or two little errors in any book I read, but it’s usually just something to note with some amusement and then move on; rarely does a misstatement or error like that cause me serious concern, and I rarely comment on them in my review of a book. A whole string of them, page after page, however, convinces me that the author is a sloppy writer or has a very superficial knowledge of the subject at hand. When the writer is a working scientist writing about science, I am totally confounded. As for these bigger errors I’ve just discussed — they are inexplicable. It is the author’s responsibility to realize the limits of his or her knowledge or understanding and find ways to avoid or correct problems in his or her writing.

These are the reasons why I simply cannot recommend this book to a general reader. That the book seems to have reached some level of popularity disturbs me : such poorly conceived and executed writing about science undermines the efforts of the many excellent writers about science — scientists, historians, journalists, and others — writing with more care and accuracy about their subject.
———-
^* Michio Kaku, Physics of the impossible : a scientific exploration into the world of phasers, force fields, teleportation, and time travel. New York : Doubleday, 2008. xxi + 329 pages.

Rainbows of his Mind

My interest is captivated by this item from Mike Tidmus [source ; his post has the links]:

San Diego’s least meteorologically-inclined Christian, James Hartline, claims an airplane was struck by lightning because it flew through a rainbow — the universal symbol of gay and lesbian rights. That offense, apparently, pissed off Hartline’s god. Tweets San Diego’s Most Oppressed Christian™: “Video captures plane being struck by lightning as it flew through rainbow during catastrophic storm in San Diego. http://bit.ly/ewQxO6.”

It’s fascinating because rainbows, while they have an objective physical existence, are not tangible objects. They are optical phenomena created by sunlight refracting through a mist of water droplets and creating the image of a rainbow in the eye of observers located in the right spot to see it. The rainbow is a personal thing, created for everyone who sees it, although it indeed has an objective existence that can be measured by instruments and photographed by cameras. Nevertheless, there is no physical rainbow that one can locate in space, there is no physical rainbow that one can touch, there is no physical rainbow at the end of which one will ever find a pot of gold–but it makes a fine metaphor for the futility of such a financial quest.

In particular, there is no physical rainbow that an airplane can fly through even if it were miraculously ordained by Mr. Hartline’s invisible friend. It is of course possible that a video camera might see an airplane appear to fly through a rainbow and be struck by lightning, but it would be a very personal revelation for that videographer since someone standing nearby could watch the airplane fly comfortably past the rainbow.

Still other observers standing elsewhere would be in the wrong place to see the rainbow but they could still observe the airplane, perhaps seeing it struck by lightning as it flew over Mr. Hartline’s head. What a revelation a change in perspective can bring!

Perpetually Park

Bob Park, in his “What’s New” this week (5 March 2010) had two items on perpetual-motion machines, an idea, like creationism, that seems not to go away but just to get repackaged on a regular basis, said new packaging bagging lots of new, credulous believers–rather like creationism.

I particularly enjoyed ‘it’s not a perpetual motion machine, but it’s “so efficient that it keeps on producing power when it’s unhooked from an outside power source.”‘ Wow.

As for the case law on perpetual motion machines, you’d think that the second law of thermodynamics might be enough but apparently reality is not a form of legal truth.

2. MANNA: ISN’T THAT A GIFT FROM HEAVEN?
The town of Odessa, MO, population 4,818, located somewhere east of Kansas City, needs jobs. So when a company, Manna of Utah, said it wanted to build a plant there employing 3000 people, folks cheered. All the town had to do was provide $90 million in revenue bonds and a site. The company even flew local officials to Florida for a demonstration of the “world-changing” technology that would be built there. It’s a home generator developed by Maglev Energy in Largo, Florida, which is leasing the technology to Manna of Utah. State Representative Mike McGhee (R-Odessa) said the product would be the “equivalent of the light bulb.” Steve Everly of the Kansas City Star thought it might be a good idea to check with scientists and engineers, including Bob Park. The mayor of Odessa, Tony Bamvakais, who went on the trip to Florida, says it’s not a perpetual motion machine, but it’s “so efficient that it keeps on producing power when it’s unhooked from an outside power source.”

3. PATENT NONSENSE: CASE LAW ON PERPETUAL MOTION MACHINES.
When Joseph Newman was refused a patent for his Energy Machine he sued the US patent office. Legendary US District Court Judge Robert Penfield Jackson ordered Newman to turn his machine over to the National Bureau of Standards for testing. It was found to be a motor/generator of a design vastly inferior to those on the market. The case, Newman v. Quigg (Quigg was the patent Commissioner) is cited as case-law giving the patent office authority to reject perpetual-motion claims out of hand. The only effect is that they are no longer called “perpetual motion machines.” They are called over-unity devices, or zero-point-energy machines. Coverage of the Joe Newman case in Wikipedia is terrible. It’s a remarkably useful encyclopedia, but you need to verify.

95 – 21 = ?

This is a fine development in UK news for people LGBTness, but my interest in this excerpt is in the second sentence/paragraph:

The House of Lords voted to lift the ban on civil partnership ceremonies in churches and other religious premises last night.

Peers voted by 95 to 21 – a majority of 74 – to lift the ban which previously prevented gays and lesbians from getting “married” in such places.

[from Mary Bowers, "Peers vote for church civil partnership ceremonies", TimesOnline [UK], 3 March 2010.]

Is it just me or is it odd to have the newspaper doing subtraction for us?

Maybe it’s my internal physicist, maybe it’s because I like numbers, or maybe it’s just my personality as a secret stair-counter, but whenever I read or hear an assertion with numbers, some sort of calculation usually happens in my head. I don’t think I’m alone on this.

“Hmm,” I think, “95 to 21, that’s a majority of 74 out of 116 peers, close to a 75% majority.” This usually gets one more refinement — 74% if it were a 100, but it’s 16% more than 100 so subtract about 15% of 74 from 74 gives about 63 — so let’s say about 63%. Not a bad majority.

Did I learn somewhere along the way always to calculate percentages or fractions when I’m given two numbers as input?

Okay, so I realize that quite a few people feel uncomfortable around fractions and percentages, although I’d like them not to. But isn’t addition and subtraction pretty much within the comfort level of most readers of that newspaper article?

So that leaves me trying to understand why the author (or, perhaps, editors), felt it necessary to subtract 21 from 95 in print.

Equality Advances, Pie Charts Decline

Via Joe.My.God I learn that a new CBS News / New York Times poll shows an amazing 42% of those polled in favor of legal marriage for same-sex couples. That’s amazing because the previous poll by the same group only one month ago found only 33% in favor of legal marriage. This increase of 9 points lies well outside the sampling error of the poll and must represent some significant fall-out from the addition of Iowa and Vermont to the growing list of states with marriage equality.

That’s interesting enough, but this graphic from CBS (source for graphic and poll results) is also interesting:

One thing to note is that fully two-thirds of those polled support some sort of legal recognition for same-sex couples.

The other thing to note is that there is a 5% wedge missing from the pie chart. Add up the percentages and you get 95%. Now, while it is not at all unusual to have some 5% of those asked who are undecided or who wish to give no opinion, it is not kosher to leave them out of the pie chart and sort of fudge the other wedges around to fill in the space.

Does this chart make it clear that there is a 5% wedge unaccounted for? Not at all. Somehow the wedges are made to look as though they fill 100% of the circle and yet they should not. You might think that 5% is small and wouldn’t be visible, but it amounts to one-fifth of the “civil unions” wedge, an amount that would be quite noticeable. So, the chart is inaccurate and misleading. I wonder which wedge, or wedges, got the undecideds?

Shame on CBS. I hate it when big corporations who could have science and math consultants without even noticing the cost can’t be bothered.
—–
[Updated a few minutes later:] In thinking about the poll results and the remarkable shift since the previous poll, Timothy Kincaid at Box Turtle Bulletin (“Americans Shift Sharply in Favor of Marriage“) gives a long list of significant steps that have been taken towards marriage equality in the interval between the polls.

McCain’s Dangerous Science Illiteracy

At the most recent presidential so-called “debate” (that would be debate #2, the “town hall meeting” format), John McCain, trying to score cheap points against rival Barack Obama, referred to earmark money Obama voted for that included “$3 million for an overhead projector at a planetarium in Chicago, Illinois”.

Of course, as many of us knew at the time, and as many, many more now know, that “overhead projector” was actually a sophisticated piece of optical equipment, a Zeiss Mark VI star projector, the programmable star projector that recreates a view of the heavens on the ceiling of planetariums. These instruments are slightly different from an “overhead projector”.

The Adler Planetarium even felt the need to defend its honor with a press release commenting on the issues. From that press release:

To clarify, the Adler Planetarium requested federal support – which was not funded – to replace the projector in its historic Sky Theater, the first planetarium theater in the Western Hemisphere. The Adler’s Zeiss Mark VI projector – not an overhead projector – is the instrument that re-creates the night sky in a dome theater, the quintessential planetarium experience. The Adler’s projector is nearly 40 years old and is no longer supported with parts or service by the manufacturer. It is only the second planetarium projector in the Adler’s 78 years of operation.

Science literacy is an urgent issue in the United States. To remain competitive and ensure national security, it is vital that we educate and inspire the next generation of explorers to pursue careers in science, echnology, engineering and math.

My bold, of course, to highlight why you should support Ars Hermeneutica’s mission.

McCain’s science illiteracy, as illustrated by this remarkably foolish gambit, is dangerous enough. (Either he didn’t know, or he did know and willfully used this tasty sound-bite about the “overhead projector” to prey on the electorate’s illiteracy.) However, I’m sure that he didn’t come up with this earmark tidbit–someone on his staff did. Someone on McCain’s staff should have been able to say “Wait a minute, John. That’s not an overhead projector–that’s one of those really expensive, complicated planetarium thingies!”

We can’t afford scientifically illiterate leaders, nor can we afford scientific illiteracy among their staff.

As we are inclined to say at Ars: “C’mon, it’s not as if it’s rocket science we’re talking about!”

Park on EMF Non-Dangers

Just in case you came in late, or you don’t remember the events of the time, and never realized the terror that could be induced by toasters, Robert Park updates us on the utter lack of danger associated with electromagnetic fields (EMF).

HYBRIPHOBIA: REMEMBER WHEN POWER LINES CAUSED CANCER?
EMF stopped causing cancer in 1997, but no one bothered to tell Jim Motavalli, who wrote an Automobile column in the Sunday New York Times about the risks of EMF in hybrids. According to Motavalli the National Cancer Institute studied the cancer risks associated with electromagnetic fields. And so it did – but it couldn’t find any. You might think Motavalli would at least check the Archives of the New York Times. On July 3, 1997, the day the massive four-year NCI study of power lines and cancer appeared in the New England Journal of Medicine, Gina Kolata reported in the Times that the study was unambiguous and found no health effects associated with electromagnetic fields. An editorial in the same issue of the Journal put it in perspective: “Hundreds of millions of dollars have gone into studies that never had much promise of finding a way to prevent the tragedy of cancer in children. It is time to stop wasting our research resources.” It all began in 1979 when Nancy Wertheimer, an unemployed epidemiologist, and her friend Ed Leeper, drove around Denver looking for common environmental factors in the homes of childhood victims of leukemia. It practically jumped out at them – every home had electricity. Their study was so flawed it would have been laughed off but for Paul Brodeur, a scientifically-ignorant writer for The New Yorker. He wrote a series of terrifying articles about power lines and cancer that were collected in a 1989 book, Currents of Death.

[Robert Park, What's New, 2 May 2008.]

Differences in Celsius & Fahrenheit

Here’s an unexpected bit of innumeracy.

I’m about to finish up a book by Colin Tudge called The Time Before History : A Million Years of Human Impact (New York : Scribner, 1996; 366 pages). I expect there will be a book note soonish.

Anyway, here are two quotations from two nearby pages. See if you spot the problem.

We know, too, as related in chapter 2, that when the ice ages ended, they could, in any one place, end fast. Twenty years could see a 7°C (44°F) rise in temperature; the difference between a frozen landscape and a temperate one. [p. 301]

Besides, at the trough of the last ice age, 18,000 years ago, the surface of the sea in the eastern Mediterranean is known to have cooled by more than 6°C (43°F), which in ecological terms is huge, and yet the elephants and their miniaturized neighbors came through those harsh times. [p. 302]

Your reaction may be different, but the author’s–or editor’s!–error in converting the temperature differences from Celsius to Fahrenheit stands out to me as though written in flashing neon. Could they really believe that the temperature of the Mediterranean had changed by an amazing 43°F? “Huge” is one thing, but that’s huge!

Not so long ago I wrote at excessive length about how to convert values on one temperature scale to values on the other. What I didn’t talk about was how to compare temperature differences.

Look again at the formula for converting Celsius temperatures to Fahrenheit temperatures:

If we talk a bit about this equation, there are two things that it is telling us:

1. That Celsius degrees are bigger, nine-fifths bigger, than Fahrenheit degrees, which means that it takes fewer Celsius degrees to express a temperature change than Fahrenheit degrees; and
2. That the zero points on the two scales are offset by 32°F.

But this equation and this explanation refer to converting temperature values on one scale to the other. If we want to talk about temperature differences, that’s another matter, and that’s why it’s good to talk/think about what the equation above is saying.

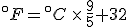
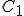Suppose we have two temperature values specified on the Celsius scale; call them and 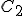. Then, to find the corresponding temperature difference expressed in terms of Fahrenheit degrees, we need to write down these two equations: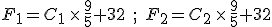

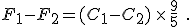
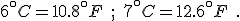
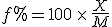
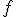and then subtract one from the other. Do the algebra and you find

You’ll notice that the offset value of 32 disappears when you do the subtraction. This is as we expected because we had just talked about how Celsius degrees are nine-fifths bigger than Fahrenheit degrees.

But now you can see the error made by the author or his editor: they erroneously used the equation to convert temperatures on the Celsius scale to temperatures on the Fahrenheit scale, rather than merely change a temperature difference from degrees of one size to degrees of another size.

The innumeracy aspect is that, before using the conversion equation, one should know what it is saying. This simple step would alert anyone that 6°C could never be 43°F. Knowing that Celsius degrees are nine-fifths bigger than Fahrenheit degrees let’s us write the correct values for these temperature differences immediately:

Bodin on Heliocentrism

After Copernicus published De Revolutionibus in 1543, acceptance of the idea that the Earth orbited the Sun was neither immediate nor universal. Some appealed to common sense:

No one in his senses, or imbued with the slightest knowledge of physics will ever think that the earth, heavy and unwieldy from its own weight and mass, staggers up and down around its own centre and that of the sun; for at the slightest jar of the earth, we would see cities and fortresses, towns and mountains thrown down.
– Jean Bodin (1529–1596), quoted in Peter Watson, Ideas, (New York : HarperCollins, 2005), p. 517

Isn’t it interesting how some common sense becomes uncommon.

GetPercent

The website GetReligion discusses press coverage of news stories about religion, and how well they exhibit an understanding of the religious issues involved. Their name comes from the idea that “The press…just doesn’t get religion.”

Well, in this little example I’m afraid there’s a bit of a need for some GetMath. In a story called “Define social justice — give at least one example“, Mark Stricherz is discussing a story about Jeremiah Wright Jr., the pastor of the church Barack Obama belongs to. I have no issues with the analysis, just with this excerpt

As Ramirez noted, plainly but aptly,

“Obama was one of the thousands who joined Trinity under Wright’s leadership. When Wright became Trinity’s pastor in 1972, the church had 85 members. Today, Trinity has a congregation of 8,500, with more than 80 ministries, making it one of the largest and most influential black churches in the nation.”

In other words, during his tenure Wright’s congregation increased by more than 1,000 percent.

Of course, one notes that Wright’s congregation increased by well over well over 1,000%. In fact, it increased by 10,000%. In other words, it increased by a factor of 100.

To move from a fractional factor, say 0.45, to an expression in percent, one multiplies by 100. Thus, 0.45 of something is also said to be 45% of that something. To move from an expression in percent to a decimal fraction, divide the percent figure by 100. Thus, 32% of something is 0.32 times that something.

This works even if the fractional part is greater than the something being compared to, it’s just that the decimal expression is greater than 1, and the percent expression is greater than 100%. This general expression

where is the percent expression, 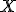is what I’ve called the fractional part, and 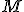is the amount being compared to, works regardless of whether the “quantity” is greater than or less than the “comparison” value.

So, in Mr. Wright’s case, his congregation, in going from 85 to 8,500 increased by a factor of 100, or by

I expect Mr. Stricherz knows this and simply mistyped, but it did provide me an excuse for a little pedantic moment of the type I love so much.