Archive for the ‘Explaining Things’ Category
Dec
24
Posted by jns on
December 24, 2010
My interest is captivated by this item from Mike Tidmus [source ; his post has the links]:
San Diego’s least meteorologically-inclined Christian, James Hartline, claims an airplane was struck by lightning because it flew through a rainbow — the universal symbol of gay and lesbian rights. That offense, apparently, pissed off Hartline’s god. Tweets San Diego’s Most Oppressed Christian™: “Video captures plane being struck by lightning as it flew through rainbow during catastrophic storm in San Diego. http://bit.ly/ewQxO6.”
It’s fascinating because rainbows, while they have an objective physical existence, are not tangible objects. They are optical phenomena created by sunlight refracting through a mist of water droplets and creating the image of a rainbow in the eye of observers located in the right spot to see it. The rainbow is a personal thing, created for everyone who sees it, although it indeed has an objective existence that can be measured by instruments and photographed by cameras. Nevertheless, there is no physical rainbow that one can locate in space, there is no physical rainbow that one can touch, there is no physical rainbow at the end of which one will ever find a pot of gold–but it makes a fine metaphor for the futility of such a financial quest.
In particular, there is no physical rainbow that an airplane can fly through even if it were miraculously ordained by Mr. Hartline’s invisible friend. It is of course possible that a video camera might see an airplane appear to fly through a rainbow and be struck by lightning, but it would be a very personal revelation for that videographer since someone standing nearby could watch the airplane fly comfortably past the rainbow.
Still other observers standing elsewhere would be in the wrong place to see the rainbow but they could still observe the airplane, perhaps seeing it struck by lightning as it flew over Mr. Hartline’s head. What a revelation a change in perspective can bring!
Sep
15
Posted by jns on
September 15, 2010
Someplace in my reading recently I happened upon the “memorandum opinion” in McLean v. Arkansas Board of Education (1982). My attention was drawn to it because of a remark about how it “defined science”. Well, I wouldn’t go so far as “defined” although the characteristics of the scientific enterprise are outlined, and that may have been a first for American jurisprudence (but I haven’t made a study of that history yet).
Judge William R. Overton summarizes the case succinctly in his introduction:
On March 19, 1981, the Governor of Arkansas signed into law Act 590 of 1981, entitled “Balanced Treatment for Creation-Science and Evolution-Science Act.” The Act is codified as Ark. Stat. Ann. &80-1663, et seq., (1981 Supp.). Its essential mandate is stated in its first sentence: “Public schools within this State shall give balanced treatment to creation-science and to evolution-science.” On May 27, 1981, this suit was filed (1) challenging the constitutional validity of Act 590 on three distinct grounds.
[source]
The grounds were 1) that it violated the establishment clause of the First Amendment to the US Constitution; 2) that it violates a right to academic freedom guaranteed by the First Amendment; and 3) that it is impermissibly vague and thereby violates the Due Process Clause of the Fourteenth Amendment.
The judge ruled in favor of plaintiffs, enjoining the Arkansas school board “from implementing in any manner Act 590 of the Acts of Arkansas of 1981″. So, there is where so-called “scientific creationism” was pushed back out of the scientific classrooms, and the reason creationists began–yet again–with rebranding and remarketing creationism, this time as “intelligent-design” creationism, to try to wedge it back into the scientific curriculum.
The opinion is refreshingly brief and to the point. It’s difficult to avoid the impulse simply to quote the whole thing.
In his discussion of the strictures of the “Establishment of Religion” clause, Judge Overton quotes from opinions by Supreme-Court Justices Black and Frankfurter
The “establishment of religion” clause of the First Amendment means at least this: Neither a state nor the Federal Government can set up a church. Neither can pass laws which aid one religion, aid all religions, or prefer one religion over another. Neither can force nor influence a person to go to or to remain away from church against his will or force him to profess a belief or disbelief in any religion. No person can be punished for entertaining or professing religious beliefs or disbeliefs, for church-attendance or non-attendance. No tax, large or small, can be levied to support any religious activities or institutions, whatever they may be called, or what ever form they may adopt to teach or practice religion. Neither a state nor the Federal Government can, openly or secretly, participate in the affairs of any religious organizations or groups and vice versa. In the words of Jefferson, the clause … was intended to erect “a wall of separation between church and State.”
[Justice Black, Everson v. Board of Education (1947)]
Designed to serves as perhaps the most powerful agency for promoting cohesion among a heterogeneous democratic people, the public school must keep scrupulously free from entanglement in the strife of sects. The preservation of the community from divisive conflicts, of Government from irreconcilable pressures by religious groups, or religion from censorship and coercion however subtly exercised, requires strict confinement of the State to instruction other than religious, leaving to the individual’s church and home, indoctrination in the faith of his choice. [Justice Frankfurter, McCollum v. Board of Education (1948)]
The phrases that jump out at me are “means at least this” and ” the public school must keep scrupulously free from entanglement in the strife of sects”. He also quotes Justice Clark (Abbington School District v. Schempp (1963)) as saying “[s]urely the place of the Bible as an instrument of religion cannot be gainsaid.”
Put them together and it’s quite clear, as Judge Overton wrote, that “[t]here is no controversy over the legal standards under which the Establishment Clause portion of this case must be judged.” Of course, this doesn’t keep certain christianist sects from repeatedly trying to assert that their version of a holy book is somehow an American historical and cultural book and not an “instrument of religion”. To the objective observer, of course, those repeated attempts merely underscore the importance and continuing relevance of vigilance in keeping schools “scrupulously free from entanglement in the strife of sects”.
Judge Overton begins section II this way:
The religious movement known as Fundamentalism began in nineteenth century America as part of evangelical Protestantism’s response to social changes, new religious thought and Darwinism. Fundamentalists viewed these developments as attacks on the Bible and as responsible for a decline in traditional values.
He continues with more brief historical notes about “Fundamentalism” (NB. his remark that it traces its roots to the nineteenth century) and its renewed concerns with each passing generation that America is finally succumbing to secularism and its civilization is at last crumbling, paralleling the conviction of millennialists that their longed for second coming of Jesus is forever imminent. Perhaps needless to say, since I am a scientist, I’d like to see predictions about the second coming and the end of civilization given a time limit so that, when said events fail to materialize in the required time, we can consider the parent theories to be disproven.
In particular he notes that fundamentalist fever was pervasive enough that teaching evolution was uncommon in schools from the 1920s to the 1960s; sentiment and practice only changed as a response to Sputnik anxiety in the early 1960s, when curricula were revamped to emphasize science and mathematics. In response, the concepts of “creation science” and “scientific creationism” were invented as a way to repackage the usual anti-evolution ideas. As Judge Overton says
Creationists have adopted the view of Fundamentalists generally that there are only two positions with respect to the origins of the earth and life: belief in the inerrancy of the Genesis story of creation and of a worldwide flood as fact, or a belief in what they call evolution.
It’s a false dichotomy, of course, but is an idea heavily promoted (usually implicitly) by modern creationists. Of course, it’s a double edged sword: when creationists work so hard to instill the idea that it can only be creationism or Darwinism, they are perceived as losing big when creationism is, yet again, crossed off as a viable “science” option by the courts.
In the remainder of this section Judge Overton examines in some detail the testimony and evidence of “Paul Ellwanger, a respiratory therapist who is trained in neither law nor science.” It’s revealing stuff, demonstrating that “Ellwanger’s correspondence on the subject shows an awareness that Act 590 is a religious crusade, coupled with a desire to conceal this fact.” It’s an arrogance on the part of creationists that we’ve seen over and over again, his recommending caution in avoiding any linkage between creationism and religion and yet continually using rhetoric about Darwinism as the work of Satan. There’s more that I won’t detail here. His conclusion for this section:
It was simply and purely an effort to introduce the Biblical version of creation into the public school curricula. The only inference which can be drawn from these circumstances is that the Act was passed with the specific purpose by the General Assembly of advancing religion.
In a nice rhetorical flourish, Judge Overton echoes this conclusion in the opening of section III:
If the defendants are correct and the Court is limited to an examination of the language of the Act, the evidence is overwhelming that both the purpose and effect of Act 590 is the advancement of religion in the public schools.
Section 4 of the Act provides:
Definitions, as used in this Act:
- (a) “Creation-science” means the scientific evidences for creation and inferences from those scientific evidences. Creation-science includes the scientific evidences and related inferences that indicate: (1) Sudden creation of the universe, energy, and life from nothing; (2) The insufficiency of mutation and natural selection in bringing about development of all living kinds from a single organism; (3) Changes only within fixed limits of originally created kinds of plants and animals; (4) Separate ancestry for man and apes; (5) Explanation of the earth’s geology by catastrophism, including the occurrence of a worldwide flood; and (6) A relatively recent inception of the earth and living kinds.
- (b) “Evolution-science” means the scientific evidences for evolution and inferences from those scientific evidences. Evolution-science includes the scientific evidences and related inferences that indicate: (1) Emergence by naturalistic processes of the universe from disordered matter and emergence of life from nonlife; (2) The sufficiency of mutation and natural selection in bringing about development of present living kinds from simple earlier kinds; (3) Emergence by mutation and natural selection of present living kinds from simple earlier kinds; (4) Emergence of man from a common ancestor with apes; (5) Explanation of the earth’s geology and the evolutionary sequence by uniformitarianism; and (6) An inception several billion years ago of the earth and somewhat later of life.
- (c) “Public schools” means public secondary and elementary schools.
The evidence establishes that the definition of “creation science” contained in 4(a) has as its unmentioned reference the first 11 chapters of the Book of Genesis. Among the many creation epics in human history, the account of sudden creation from nothing, or creatio ex nihilo, and subsequent destruction of the world by flood is unique to Genesis. The concepts of 4(a) are the literal Fundamentalists’ view of Genesis. Section 4(a) is unquestionably a statement of religion, with the exception of 4(a)(2) which is a negative thrust aimed at what the creationists understand to be the theory of evolution (17).
Both the concepts and wording of Section 4(a) convey an inescapable religiosity. Section 4(a)(1) describes “sudden creation of the universe, energy and life from nothing.” Every theologian who testified, including defense witnesses, expressed the opinion that the statement referred to a supernatural creation which was performed by God.
Defendants argue that : (1) the fact that 4(a) conveys idea similar to the literal interpretation of Genesis does not make it conclusively a statement of religion; (2) that reference to a creation from nothing is not necessarily a religious concept since the Act only suggests a creator who has power, intelligence and a sense of design and not necessarily the attributes of love, compassion and justice (18); and (3) that simply teaching about the concept of a creator is not a religious exercise unless the student is required to make a commitment to the concept of a creator.
The evidence fully answers these arguments. The idea of 4(a)(1) are not merely similar to the literal interpretation of Genesis; they are identical and parallel to no other story of creation (19).
Judge Overton continues to draw connections between the act’s definition of creation science, coupled with testimony, and it’s undeniable connections to religious doctrine and its lack of identifiable standing as anything that might conceivably be identified as “science”. He also examines, and denies, the creationists’ false dichotomy that I mentioned above that the origin of humankind must be described either by Darwinism or creationism.
And then he makes these exceptionally straightforward assertions:
In addition to the fallacious pedagogy of the two model [false dichotomy] approach, Section 4(a) lacks legitimate educational value because “creation-science” as defined in that section is simply not science. Several witnesses suggested definitions of science. A descriptive definition was said to be that science is what is “accepted by the scientific community” and is “what scientists do.” The obvious implication of this description is that, in a free society, knowledge does not require the imprimatur of legislation in order to become science.
More precisely, the essential characteristics of science are:
(1) It is guided by natural law;
(2) It has to be explanatory by reference to natural law;
(3) It is testable against the empirical world;
(4) Its conclusions are tentative, i.e. are not necessarily the final word; and
(5) Its is falsifiable. (Ruse and other science witnesses).
Creation science as described in Section 4(a) fails to meet these essential characteristics. First, the section revolves around 4(a)(1) which asserts a sudden creation “from nothing.” Such a concept is not science because it depends upon a supernatural intervention which is not guided by natural law. It is not explanatory by reference to natural law, is not testable and is not falsifiable (25).
If the unifying idea of supernatural creation by God is removed from Section 4, the remaining parts of the section explain nothing and are meaningless assertions.
Section 4(a)(2), relating to the “insufficiency of mutation and natural selection in bringing about development of all living kinds from a single organism,” is an incomplete negative generalization directed at the theory of evolution.
Section 4(a)(3) which describes “changes only within fixed limits of originally created kinds of plants and animals” fails to conform to the essential characteristics of science for several reasons. First, there is no scientific definition of “kinds” and none of the witnesses was able to point to any scientific authority which recognized the term or knew how many “kinds” existed. One defense witness suggested there may may be 100 to 10,000 different “kinds.” Another believes there were “about 10,000, give or take a few thousand.” Second, the assertion appears to be an effort to establish outer limits of changes within species. There is no scientific explanation for these limits which is guided by natural law and the limitations, whatever they are, cannot be explained by natural law.
The statement in 4(a)(4) of “separate ancestry of man and apes” is a bald assertion. It explains nothing and refers to no scientific fact or theory (26).
Section 4(a)(5) refers to “explanation of the earth’s geology by catastrophism, including the occurrence of a worldwide flood.” This assertion completely fails as science. The Act is referring to the Noachian flood described in the Book of Genesis (27). The creationist writers concede that any kind of Genesis Flood depends upon supernatural intervention. A worldwide flood as an explanation of the world’s geology is not the product of natural law, nor can its occurrence be explained by natural law.
Section 4(a)(6) equally fails to meet the standards of science. “Relatively recent inception” has no scientific meaning. It can only be given in reference to creationist writings which place the age at between 6,000 and 20,000 years because of the genealogy of the Old Testament. See, e.g., Px 78, Gish (6,000 to 10,000); Px 87, Segraves(6,000 to 20,000). Such a reasoning process is not the product of natural law; not explainable by natural law; nor is it tentative.
“Creation science…is simply not science.” Now, there’s an unequivocal statement! This was a very clear death knell for creationism in its guise as “creation [so-called] science” and the beginnings of the ill-concealed attempt to rebrand religious creationism, this time as “intelligent design”.
Please note that the five “characteristics of science” given above by Judge Overton are in no way a “definition” of science, which only reinforces my own impression that Judge Overton was thinking very, very clearly on the subject. I am quite ready to agree with him that the five things he lists are indeed characteristic of science. It is not a comprehensive list, and it doesn’t claim to be a comprehensive list–another thoughtful and precise step on Judge Overton’s part–but they are correct, precise, and enough in this last section of his opinion to counter very thoroughly the claims of creationism to being a science.
This gets us about halfway through Judge Overton’s opinion and this listing of some “characteristics of science”, and I’ll stop here. Before I read the opinion I feared, based on the evidently casual and inaccurate comment that led me to it, that the Judge may indeed have tried to “define” science, a difficult task that I was convinced hardly belonged in court proceedings. I was delighted to discover that Judge Overton instead developed careful and precise “characteristics of science” that served the purpose of the court and are undeniably correct.
Dec
21
Posted by jns on
December 21, 2009
I am always happy to celebrate the decision of our sun to return to a higher point in our northern sky, a decision it routinely takes about this time of year: 21 December. It seems so delightful that the days seem to start getting longer immediately it makes the decision.
And then, whenever the topic comes up, as it certainly has today, I always make a pest of myself by pointing out my favorite astronomical fact for those of us in the northern hemisphere: although the winter solstice marks the shortest amount of daylight in the year, the earliest sunset of the year actually happened three weeks ago, on 7 December. The last time I mentioned it in this space (in 2006) I didn’t have any really good, clear explanation to offer and I don’t this time, either. I posted a few links previously — look at them if you feel yourself the intrepid explorer of orbital dynamics — but for now we’ll just wave our hands and say it’s because of the tilt of the Earth, and the fact that it’s roughly spherical (at least, I think this would not happen if the Earth were cylindrical along its axis of rotation).
But anyway, the point I always make is this: by the time we get to the solstice, the sunset is already getting noticeably later and psychologically (to me, at least, since I rarely encounter sunrise) this makes us feel the day is getting longer at a rather brisk pace once the solstice is passed. The reason for that sensation, of course, is that it started three weeks ago. (Have fun verifying this for yourself with the NOAA Sunrise/Sunset calendar.)
For those who key on the sunrise to judge the length of their day–I’m sorry, but the latest sunrise falls on 7 January.
Sep
03
Posted by jns on
September 3, 2009
 I did not plan to become the expert on such an arcane topic–although I can answer the question as it arises–but once I had written a blog posting called “Atoms Are Not Watermelons“,* my web was spun, my net set, the trap was ready for the unsuspecting googler who should type such an interesting question as
I did not plan to become the expert on such an arcane topic–although I can answer the question as it arises–but once I had written a blog posting called “Atoms Are Not Watermelons“,* my web was spun, my net set, the trap was ready for the unsuspecting googler who should type such an interesting question as
Are the atoms in a watermelon the same as usual atoms?
Perhaps you don’t find this question as surprising as I do. However, since I am the number-one authority on the atoms in watermelons, at least according to the google,‡ I deem the question worth answering and I will answer it.
The answer to the question: yes. The atoms in a watermelon are definitely the same as the usual atoms.
It is, in fact, the central tenet of the atomic theory that everything in the universe is made from the same constituent particles that we know as “elements”, except for those things that are not made of atoms (subatomic particles, for instance, or neutron stars). Even in the most distant galaxies where there are atoms they are known to be the familiar atomic elements.
Watermelon (Citrullus lanatus) is about 92% water, 6% sugar (both by weight). Thus, by number, the vast majority of atoms in a watermelon are hydrogen, oxygen, and carbon. There are also organic molecules as flavors, amino acids and vitamins, plus trace elemental minerals like iron, magnesium, calcium, phosphorus, potassium, and zinc.
The USDA tells us that “Watermelon Packs a Powerful Lycopene Punch“, saying
Lycopene is a red pigment that occurs naturally in certain plant and algal tissues. In addition to giving watermelon and tomatoes their color, it is also thought to act as a powerful antioxidant. Lycopene scavenges reactive oxygen species, which are aggressive chemicals always ready to react with cell components, causing oxidative damage and loss of proper cell function.
I was interested to discover that one can even buy watermelon powder and Lycopene powder, both from the same source, Alibaba.com, which seems to be a diversified asian exporter.
By request from Isaac, here are some recipes for pickled watermelon rind (about which he says “I’ve always wanted to make it.” I never knew — and after 17 years living with someone you’d think I’d have found out):
- Sweet Pickled Watermelon Rind — most of the recipes that I turned up seemed to be variations on this sweet version, said to be a traditional “Southern” style of some indeterminate age; I’ve not located the ur-recipe yet. Some gussy it up, many vary the amounts of the ingredients while maintaining the same proportions, and one I read added 4 sliced lemons to the pot, which sounded like a nice variation.
- Watermelon Rind Pickles — this is the not sweet, more pickley version that I think I would find more to my taste. This recipe makes “fresh” pickle, simply stored in the refrigerator, versus processed & canned pickle as in the previous recipe.
———-
* Having just read Richard Rhodes’ How to Write, the subject at hand was bad metaphors in science writing, which he expressed by saying “atoms are not watermelons”.
‡ Oddly, Yahoo! and Bing do not agree, more their loss.
Aug
20
Posted by jns on
August 20, 2009
 This is the youthful Galileo Galilei (1564–1642), who established the intellectual starting point for this short discussion.
This is the youthful Galileo Galilei (1564–1642), who established the intellectual starting point for this short discussion.
In Galileo’s day [c. 1610], the study of astronomy was used to maintain and reform the calendar. Sufficiently advanced students of astronomy made horoscopes; the alignment of the stars was believed to influence everything from politics to health.
[David Zax, "Galileo's Vision", Smithsonian Magazine, August 2009.*]
Galileo published The Starry Messenger (Sidereus Nuncius), the book in which he reported his discovery of four new planets (i.e., moons) apparently orbiting Jupiter, in 1610. This business of looking at things and reporting on observations just didn’t fit well with the prevailing Aristotelian view of nature and the way things were done.
Some of his contemporaries refused to even look through the telescope at all, so certain were they of Aristotle’s wisdom. “These satellites of Jupiter are invisible to the naked eye and therefore can exercise no influence on the Earth, and therefore would be useless, and therefore do not exist,” proclaimed nobleman Francesco Sizzi. Besides, said Sizzi, the appearance of new planets was impossible—since seven was a sacred number: “There are seven windows given to animals in the domicile of the head: two nostrils, two eyes, two ears, and a mouth….From this and many other similarities in Nature, which it were tedious to enumerate, we gather that the number of planets must necessarily be seven.”
[link as above]
Science as a an empirical pursuit was still a new idea, quite evidently.
At the time it was understood, for various “obvious” reasons (one of them apparently being that they could be seen), that the planets and the stars in the nearby “heavens” (rather literally) influenced things on Earth. There was no known reason why or how, but this wasn’t a big issue because causality‡ didn’t play a very large role in scientific explanations of the day. Recall, for instance, that heavier objects rushed faster to tall to Earth because it was their nature to do so.
What I suddenly realized awhile back (I was reading the book by Robert P, Crease, Great Equations, but I don’t really remember what prompted the thoughts) is the following.
Received mysticism today claims that astrology, the practice of divination through observation of the motions of the planets, operates through the agency of some unknown, mysterious force as yet unknown to science. Science doesn’t know everything!
But this is wrong. In the time of Galileo there was no known “force” to serve as the “cause” for the planets’ effect on human life, but it seemed quite reasonable. In fact, the idea of “force” wasn’t yet in the mental frame. The notion of “force” as it is familiar to us today only began to take shape with the work of Isaac Newton c. 1687, when he published his Philosophiae Naturalis Principia Mathematica, which contained his theories of mechanics and gravitation, theories where the idea of “force” began to take shape, and to develop the ideas of causality.
But the notion that there is no known mechanism through which astrology might work we now see is wrong. The mechanism, arrived at by Newton, which handily explained virtually everything about how the planets moved and exerted their influence on everything in the known universe, was that of universal gravitation.
The one thing that universal gravitation did not explain was astrology. But even worse, this brilliant theory showed that the universal force behind planetary interaction and influence was much, much too small to have any influence whatsoever on humans and their lives.
Newton debunked astrology over 300 years ago by discovering its mechanism and finding that it could not possibly have the influence that its adherents claimed.
Some people, of course, are a little slow to catch up with modern developments.
———-
* This is an interesting article that accompanies a virtual exhibit, “Galileo’s Instruments of Discovery“, adjunct to a physical exhibit at the Franklin Institute (Philadelphia).
‡ Perhaps it would be more accurate to say that our modern notion of causes was quite a bit different from 15th century notions of causes.
Jun
09
Posted by jns on
June 9, 2009
 This is* author John R. Gribbin (1946– ), a science writer who started life as an astrophysicist. (His website.) I’ve read and mentioned a few of his books here in the last year or so, and I’ve been enjoying them so far.
This is* author John R. Gribbin (1946– ), a science writer who started life as an astrophysicist. (His website.) I’ve read and mentioned a few of his books here in the last year or so, and I’ve been enjoying them so far.
The one that I most recently read and enjoyed is John Gribbin with Mary Gribbin, Stardust : Supernovae and Life—The Cosmic Connection (New Haven, Yale University Press, 2000. xviii + 238 pages). Here is my book note.
The book is all about stellar nucleosynthesis: how the elements are made in stars and supernovae. As you may have realized, this is a subject I find fascinating, particularly the history of the discovery of nucleosynthesis. I’m especially keen on the late nineteenth controversy about the age of the sun, a controversy starring two big names in science, Darwin and Lord Kelvin, a controversy that couldn’t be settled until the invention of quantum mechanics and the discovery of nuclear fusion.
That problem was finally cracked by Hans Bethe in two papers he published in 1939 in Physical Review (“Energy Production in Stars”, first paper online, and second paper online. A very nice short, nontechnical summary of the importance of these papers (“Landmarks: What Makes the Stars Shine?“) is also available online. I may have to write more about these sometime.
But the excerpt from Stardust that I wanted to share here has to do with a different question, one that came up in a discussion we had elsewhere (“Long Ago & Far Away“) following a question Bill asked about the size of the expanding universe.
This doesn’t address that question directly, but does answer another related question. I was unclear at the time whether celestial red-shift should be interpreted as the result of actual motion of objects in the universe apart from each other, or as the result of the expansion of space-time itself, or some combination.
The answer is unequivocal in this excerpt: red-shifts are due to expanding space-time. That is, the geometry of space-time itself is stretching out and this is what causes the apparent motion of cosmic objects away from us (with some actual relative motion through space-time going on).
Hard though it may be to picture, what the general theory of relativity tells us is that space and time were born, along with matter, in the precursor to the Big Bang, and that this bubble of spacetime full of matter and energy (the same thing—remember E = mc2) has expanded ever since. The galaxies fill the Universe today, and the matter they contain always did fill the Universe, although obviously the pieces of matter were closer together when the Universe was smaller. Since the cosmological redshift is caused not by galaxies moving through space but by space itself expanding in between the galaxies, it is certainly not a Doppler effect, and it isn’t really measuring velocity, but a kind of pseudo-velocity. Partly for historical reasons, partly for convenience, astronomers do, though, continue to refer to the “recession velocities” of distant galaxies, although no competent cosmologist ever describes the cosmological redshift as a Doppler effect. [p. 116]
———-
* The source of the photo is an (undated) article from American Scientist, “Scientists’ Nightstand: John Gribbin“, by Greg Ross, which has an interview with Gribbin and gives this thumbnail biography:
John R. Gribbin studied astrophysics at the University of Cambridge before beginning a prolific career in science writing. He is the author of dozens of books, including In Search of Schrödinger’s Cat (Bantam, 1984), Stardust (Yale University Press, 2000), Ice Age (with Mary Gribbin) (Penguin, 2001) and Science: A History (Allen Lane, 2002).
May
27
Posted by jns on
May 27, 2009
 This* is Scottish physicist James Clerk Maxwell (1831–1879). He did significant work in several fields (including statistical physics and thermodynamics, in which I used to research) but his fame is associated with his electromagnetic theory. Electromagnetism combined the phenomena of electricity and magnetism into one, unified field theory. Unified field theories are still all the rage. It was a monumental achievement, but there was also a hidden bonus in the equations. We’ll get to that.
This* is Scottish physicist James Clerk Maxwell (1831–1879). He did significant work in several fields (including statistical physics and thermodynamics, in which I used to research) but his fame is associated with his electromagnetic theory. Electromagnetism combined the phenomena of electricity and magnetism into one, unified field theory. Unified field theories are still all the rage. It was a monumental achievement, but there was also a hidden bonus in the equations. We’ll get to that.
He published his equations in the second volume of his A Treatise on Electricity & Magnetism, in 1873. I think we should look at them because they’re pretty; I suspect they’re even kind of pretty regardless of whether the math symbols convey significant meaning to you. There are four (which you may not see in Bloglines, which doesn’t render tables properly for me):
I don’t want to explain much detail at all because it’s not necessary for what we’re talking about, but there are a few fun things to point out. The E is the electric field; the B is the magnetic field.
The two equations on the top say that electric fields are caused by electric charges, but magnetic fields don’t have “magnetic charges” (aka “magnetic monopoles”) as their source. The top right equation gets changed if a magnetic monopole is ever found.
The two equations on the bottom say that electric fields can be caused by magnetic fields that vary in time; likewise, magnetic fields can be caused by electric fields that vary in time. These are the equations that unify electricity and magnetism since, as you can easily see, the behavior of each depends on the other.
There’s one more equation to look at. A few simple manipulations with some of the equations above lead to this result:
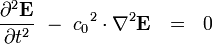
This equation has the form of a wave equation, so called because propagating waves are solutions to the equation. Maxwell obtained this result and then made a key identification. Just from its form the mathematician can see that the waves that solve this equation travel with a speed given by 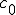 , which is related to the product of the physical constants
, which is related to the product of the physical constants  and
and 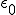 that appeared in the earlier equations.
that appeared in the earlier equations.
The values of these were known at the time and Maxwell made the thrilling discovery that this speed
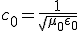
was remarkably close to the measured value of the speed of light. He concluded that light was a propagating electromagnetic wave. He was right.
That’s fine for the electromagnetism part. What’s the relationship with relativity? Let’s keep it simple and suggestive. You know from the popular lore that Einstein came up with the ideas of special relativity from thinking about traveling at the speed of light, and that the speed of light (in vacuum) is a “universal speed limit”. Only light — electromagnetic waves or photons depending on how your experiment is measuring it/them — travels at the speed of light.†
In fact, Einstein’s relativity paper (published as “Zur Elektrodynamik bewegter Körper”, in Annalen der Physik. 17:891, 1905) was titled “On the Electrodynamics of Moving Bodies”. (Read an English version here; there are no equations at the start, so read the beginning and be surprised how familiar it sounds.) That’s suggestive, don’t you think?
Speaking of special relativity, you’ve no doubt heard of the idea of an “inertial reference frame”, a concept that is central to special relativity. But, what exactly is an “inertial reference frame”?
I’m so glad you asked, since that was half the point of this post anyway. You surely realized by this time that Maxwell was partly a pretext. For our entertainment and enlightenment today we have educational films.
First, a quick introduction to the “PSSC Physics” course. From the MIT Archives:
In 1956 a group of university physics professors and high school physics teachers, led by MIT’s Jerrold Zacharias and Francis Friedman, formed the Physical Science Study Committee (PSSC) to consider ways of reforming the teaching of introductory courses in physics. Educators had come to realize that textbooks in physics did little to stimulate students’ interest in the subject, failed to teach them to think like physicists, and afforded few opportunities for them to approach problems in the way that a physicist should. In 1957, after the Soviet Union successfully orbited Sputnik , fear spread in the United States that American schools lagged dangerously behind in science. As one response to the perceived Soviet threat the U.S. government increased National Science Foundation funding in support of PSSC objectives.
The result was a textbook and a host of supplemental materials, including a series of films. In a discussion I was reading on the Phys-L mailing list recently, the PSSC course was discussed and my attention was drawn to two PSSC films that are available from the Internet Archive: “Frames of Reference” (1960) and “Magnet Laboratory” (1959). (Use these links if the embedded players below don’t render properly.) Both are very instructive and highly entertaining. Each lasts about 25 minutes.
Let’s look first at the film on magnets; it’s quite a hoot. First, the background: when I was turning into a physicist I knew some people who went to work at the “Francis Bitter National Magnet Lab” (as it was known at the time) at MIT. This was the place for high-field magnet work.
Well, this film is filmed there when it was just Francis Bitter’s magnet lab, and we’re given demonstrations by Bitter himself, along with a colleague, not to mention a tech who runs a huge electrical generation and is called either “Beans” or “Beams”–I couldn’t quite make it out. These guys have a lot of fun doing their demonstrations.
At one point in the film we hear the phone ringing. Beans calls out: “EB [?], you’re wanted on the telephone.” Bitter replies, without losing the momentum on his current demonstration, “Well, tell ‘em to call me back later, I’m busy.” Evidently multiple takes were not in the plan.
This is great stuff for people who like big machinery and big electricity and big magnets. Watch copper rods smoke while they put an incredible 5,000 amps of current through them. I laughed when Bitter started a demonstration: “All right, Beans, let’s have a little juice here. Let’s start gently. Let’s have about a thousand amps to begin with.” Watch as they melt and then almost ignite one of their experiments. It evidently happened often enough, because they have a fire extinguisher handy.
This next film on “Frames of Reference” is a little less dramatic, but the presenters perform some lovely simple but clever and illustrative experiments, demonstrations that would almost certainly be done today with computer animations so it’s wonderful to see them done with real physical objects. After they make clear what inertial frames of reference are they take a look at non-inertial frames and really clarify some issues about the fictitious “centrifugal force” that appears in rotating frames.
———-
* The photograph comes from the collection of the James Clerk Maxwell foundation.
† Duh.
Apr
02
Posted by jns on
April 2, 2009
 This is physicist and science-fiction author Gregory Benford. His official website, source of the photograph, tells us that
This is physicist and science-fiction author Gregory Benford. His official website, source of the photograph, tells us that
Benford [born in Mobile, Alabama, on January 30, 1941] is a professor of physics at the University of California, Irvine, where he has been a faculty member since 1971. Benford conducts research in plasma turbulence theory and experiment, and in astrophysics.
Around 1990, the last time I was on a sci-fi binge, I read a number of his books; I see from the official list of novels that I’m behind by a number of books. I should pick up where I left off. I remember Benford’s writing as being very satisfactory from both a science viewpoint and from a fiction viewpoint, although I find that, in my mind, I confuse some of the story-memory details with plots by the late physicist and sci-fi author Charles Sheffield, to whom I give the edge in my preference for hard-science-fiction and adventuresome plots.
But, as is not unprecedented in this forum, Mr. Benford is really providing a pretext–a worthwhile pretext on several counts, clearly, but a pretext nonetheless, because I wanted to talk about “Benford’s Law” and that Benford did not wear a beard.
Frank Benford (1883-1948) was a physicist, or perhaps an electrical engineer–or perhaps both; sources differ but the distinctions weren’t so great in those days. His name is attached to Benford’s Law not because he was the first to notice the peculiar mathematical phenomenon but because he was better at drawing attention to it.
I like this quick summary of the history (Kevin Maney, “Baffled by math? Wait ’til I tell you about Benford’s Law“, USAToday, c. 2000)
The first inkling of this was discovered in 1881 by astronomer Simon Newcomb. He’d been looking up numbers in an old book of logarithms and noticed that the pages that began with one and two were far more tattered than the pages for eight and nine. He published an article, but because he couldn’t prove or explain his observation, it was considered a mathematical fluke. In 1963, Frank Benford, a physicist at General Electric, ran across the same phenomenon, tried it out on 20,229 different sets of data (baseball statistics, numbers in newspaper stories and so on) and found it always worked.
It’s not a terribly difficult idea, but it’s a little difficult to pin down exactly what Benford’s Law applies to. Let’s start with this tidy description (from Malcolm W. Browne, “Following Benford’s Law, or Looking Out for No. 1“, New York Times, 4 August 1998):
Intuitively, most people assume that in a string of numbers sampled randomly from some body of data, the first non-zero digit could be any number from 1 through 9. All nine numbers would be regarded as equally probable.
But, as Dr. Benford discovered, in a huge assortment of number sequences — random samples from a day’s stock quotations, a tournament’s tennis scores, the numbers on the front page of The New York Times, the populations of towns, electricity bills in the Solomon Islands, the molecular weights of compounds the half-lives of radioactive atoms and much more — this is not so.
Given a string of at least four numbers sampled from one or more of these sets of data, the chance that the first digit will be 1 is not one in nine, as many people would imagine; according to Benford’s Law, it is 30.1 percent, or nearly one in three. The chance that the first number in the string will be 2 is only 17.6 percent, and the probabilities that successive numbers will be the first digit decline smoothly up to 9, which has only a 4.6 percent chance.
Take a long series of numbers drawn from certain broad sets, and look at the first digit of each number. The frequency of occurrence of the numerals 1 through 9 are not uniform, but distributed according to Benford’s Law. Look at this figure that accompanies the Times article:
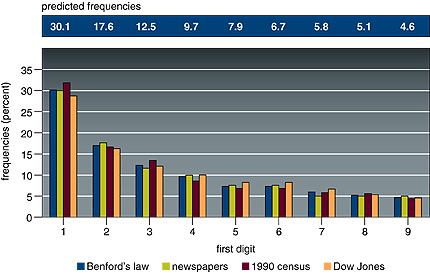
Here is the original caption:
(From “The First-Digit Phenomenon” by T. P. Hill, American Scientist, July-August 1998)
Benford’s law predicts a decreasing frequency of first digits, from 1 through 9. Every entry in data sets developed by Benford for numbers appearing on the front pages of newspapers, by Mark Nigrini of 3,141 county populations in the 1990 U.S. Census and by Eduardo Ley of the Dow Jones Industrial Average from 1990-93 follows Benford’s law within 2 percent.
Notice particularly the sets of numbers that were examined for the graph above: numbers from newspapers (not sports scores or anything sensible, just all the numbers from their front pages), census data, Dow Jones averages. These collections of numbers do have some common characteristics but it’s a little hard to pin down with precision and clarity.
Wolfram Math (which shows a lovely version of Benford’s original example data set halfway down this page) says that “Benford’s law applies to data that are not dimensionless, so the numerical values of the data depend on the units”, which seems broadly true but, curiously, is not true of the original example of logarithm tables. (But they may be the fortuitous exception, having to do with their logarithmic nature.)
Wikipedia finds that a sensible explanation can be tied to the idea of broad distributions of numbers, a distribution that covers orders of magnitude so that logarithmic comparisons come into play. Plausible but not terribly quantitative.
This explanation (James Fallows, “Why didn’t I know this before? (Math dept: Benford’s law)“, The Atlantic, 21 November 2008) serves almost as well as any without going into technical details:
It turns out that if you list the population of cities, the length of rivers, the area of states or counties, the sales figures for stores, the items on your credit card statement, the figures you find in an issue of the Atlantic, the voting results from local precincts, etc, nearly one third of all the numbers will start with 1, and nearly half will start with either 1 or 2. (To be specific, 30% will start with 1, and 18% with 2.) Not even one twentieth of the numbers will begin with 9.
This doesn’t apply to numbers that are chosen to fit a specific range — sales prices, for instance, which might be $49.99 or $99.95 — nor numbers specifically designed to be random in their origin, like winning lottery or Powerball figures or computer-generated random sums. But it applies to so many other sets of data that it turns out to be a useful test for whether reported data is legitimate or faked.
Here’s yet another graph of first digits from vastly differing sets numbers following Benford’s Law (from Lisa Zyga, “Numbers follow a surprising law of digits, and scientists can’t explain why“, physorg.com, 10 May 2007); again one should note the extreme heterogeneity of the number sets (they give “lottery” results to show that, as one truly wants, the digits are actually random):
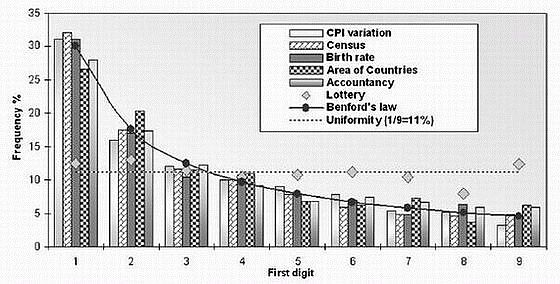
The T.P. Hill mentioned above (in the caption to the first figure), is a professor of mathematics at Georgia Tech who’s been able to prove some rigorous results about Benford’s Law. From that institution, this profile of Hill (with an entertaining photograph of the mathematician and some students) gives some useful information:
Many mathematicians had tackled Benford’s Law over the years, but a solid probability proof remained elusive. In 1961, Rutgers University Professor Roger Pinkham observed that the law is scale-invariant – it doesn’t matter if stock market prices are changed from dollars to pesos, the distribution pattern of significant digits remains the same.
In 1994, Hill discovered Benford’s Law is also independent of base – the law holds true for base 2 or base 7. Yet scale- and base-invariance still didn’t explain why the rule manifested itself in real life. Hill went back to the drawing board. After poring through Benford’s research again, it clicked: The mixture of data was the key. Random samples from randomly selected different distributions will always converge to Benford’s Law. For example, stock prices may seem to be a single distribution, but their value actually stems from many measurements – CEO salaries, the cost of raw materials and labor, even advertising campaigns – so they follow Benford’s Law in the long run. [My bold]
So the key seems to be lots of random samples from several different distributions that are also randomly selected: randomly selected samples from randomly selected populations. Whew, lots of randomness and stuff. Also included is the idea of “scale invariance”: Benford’s Law shows up in certain cases regardless of the units used to measure a property–that’s the “scale” invariance–which implies certain mathematical properties that lead to this behavior with the logarithmic taste to it.
Another interesting aspect of Benford’s Law is that it has found some applications in detecting fraud, particularly financial fraud. Some interesting cases are recounted in this surprisingly (for me) interesting article: Mark J. Nigrini, “I’ve Got Your Number“, Journal of Accountancy, May 1999. The use of Benford’s Law in uncovering accounting fraud has evidently penetrated deeply enough into the consciousness for us to be told: “Bernie vs Benford’s Law: Madoff Wasn’t That Dumb” (Infectious Greed, by Paul Kedrosky).
And just to demonstrate that mathematical fun can be found most anywhere, here is Mike Solomon (his blog) with some entertainment: “Demonstrating Benford’s Law with Google“.
Jan
19
Posted by jns on
January 19, 2009
 This is Sir William Thomson, Baron Kelvin* (1824 – 1907) or, simply, Lord Kelvin as he’s known to us in the physical sciences. This is the same “Kelvin” as in the SI unit “Kelvins”, the degrees of the absolute thermodynamic temperature scale.
This is Sir William Thomson, Baron Kelvin* (1824 – 1907) or, simply, Lord Kelvin as he’s known to us in the physical sciences. This is the same “Kelvin” as in the SI unit “Kelvins”, the degrees of the absolute thermodynamic temperature scale.
The photograph was taken c. 1900 by T. & R. Annan & Sons. I love the title given the photograph by the National Galleries of Scotland: “Sir William Thomson, Baron Kelvin, 1824 – 1907. Scientist, resting on a binnacle and holding a marine azimuth mirror”.
A binnacle, Wikipedia tells me, is a box on the deck of a ship that holds navigational instruments ready for easy reference. One reason Kelvin might be leaning on one is suggested by this bit from the article on “binnacle”
In 1854 a new type of binnacle was patented by John Gray of Liverpool which directly incorporated adjustable correcting magnets on screws or rack and pinions. This was improved again when Lord Kelvin patented in the 1880s another system of compass and which incorporated two compensating magnets.
Kelvin also patented the “marine azimuth mirror” (see the description of “azimuth mirror” from the collection of the Smithsonian National Museum of American History), so the photograph has narrative intent. It seems that Kelvin was an active and successful inventor.
I like this understated biography of Kelvin from the National Galleries of Scotland website (link in first footnote), where it accompanies the photograph:
A child prodigy, William Thomson went to university at the age of eleven. At twenty-two he was appointed Professor of Natural Philosophy in Glasgow where he set up the first physics laboratory in Great Britain and proved an inspiring teacher. He primarily researched thermodynamics and electricity. On the practical side he was involved in the laying of the Atlantic telegraph cable. He was also the partner of a Glasgow firm that made measuring instruments from his own patents.
“He primarily researched thermodynamics and electricity” is a bit of an understatement! Around the time this photograph was taken (c. 1900), Kelvin was pretty much the scientific authority in the world, the great voice of science, the scientist whose opinion on every matter scientific was virtually unassailable.
That unassailability was a huge problem for (at least) Charles Darwin and his theory of common descent by means of natural selection. The crux of the problem was the answer to this question: how old is the Earth?
These days we are quite accustomed to the idea that the Earth is around 4.5 billion years old. At the beginning of the 19th century is was very commonly believed that the Earth was only several thousand years old: Bishop Usher’s calculated date of creation, 23 October 4004 BC, was seen at the time as a scholarly refinement of what everyone already pretty much knew to be true.
Perhaps the big idea growth during the 1800s was the dawning realization of the great antiquity of the Earth. This was accompanied by the realization that fossils might actually be animal remains of some sort; the emergence of geology as a science; and the concept of “uniformitarianism” (an interesting article on the topic), so central to geology, that geological processes in the past, even the deep past, were probably very much like geological processes in action today, so that the geological history of the Earth–and of fossil remains!–could be made sense of.†
Throughout the 19th century discovery after discovery seemed to demand an ever-older Earth. I can imagine that an element of the scientific zeitgeist that precipitated Darwin’s ideas on natural selection as a mechanism for evolution was this growing realization that the Earth might be very, very, very old and that something so remarkably slow as he knew natural selection would be, might be possible. In fact, his ideas went further out on the intellectual limb: he realized that it was necessary that the Earth be much, much older than was currently thought.
In fact, he staked his reputation on the great antiquity of the Earth. This was the critical prediction of his theory, really: the Earth must be vastly older than people thought at the time or else his theory of common descent by natural selection was wrong. It was a bold, seemingly foolhardy claim that he seemed certain to lose.
He was right, of course, but things looked grim at the time and his reasoning was not vindicated by physics until well after his death.
The biggest roadblock to widespread acceptance of the idea of an Earth old enough to allow evolution of humankind through natural selection was none other than Lord Kelvin.
Calculating the age of the Earth looked at the time to be a very challenging problem. But, if there was one thing Kelvin knew, it was that the Earth could not be older than the Sun, and he believed he could calculate the age of the Sun. He was the master of physics, particularly thermodynamics, so all he had to do was add up the sources of energy that contributed to the energy we saw coming from the Sun and figure out how long it might have been going on.
But what were the sources of the Sun’s heat? Kelvin quickly concluded that it could not be any sort of chemical burning, like coal in a fireplace. There simply could not be enough coal. To keep this long story short, Kelvin finally settled on two leading possibilities. One was the energy that came from gravitation contraction of the primordial matter that formed the sun, in which case the sun heated up a great deal originally and then spent eons radiating away its heat. The other possibility that might contribute was the gravitational energy of meteors falling into the sun. (Here’s an interesting and brief exposition of the arguments: S. Gavin, J. Conn, and S. P. Karrer, “The Age of the Sun: Kelvin vs. Darwin“.)
Kelvin published his thoughts in an interesting, and very readable paper, called “On the Age of the Sun’s Heat” , Macmillan’s Magazine, volume 5 (March 5, 1862), pp. 288-293. (html version; pdf version) In the conclusion to that paper Kelvin wrote:
It seems, therefore, on the whole most probable that the sun has not illuminated the earth for 100,000,000 years, and almost certain that he has not done so for 500,000,000 years. As for the future, we may say, with equal certainty, that inhabitants of the earth can not continue to enjoy the light and heat essential to their life for many million years longer unless sources now unknown to us are prepared in the great storehouse of creation.
What an irritant for Darwin! That was not nearly enough time!
These days it is a clichéd joke to say of something that “it violates no known laws of physics”, but that’s the punchline for this entire controversy. Kelvin, naturally, had to search for sources of the Sun’s heat that violated no known laws of physics as they were known at the time, but there were new laws of physics lurking in the wings.
Darwin published On the Origin of Species in 1859. Kelvin published his paper in 1862. Radioactivity was only discovered by Henri Becquerel in 1896. The radioactive decay of elements was not recognized for some time as a possible source of solar energy, but as understanding advanced it was realized that the transmutation of one element into another through radioactive decay involved a loss of mass–the materials before and after could be weighed.
The next domino fell in 1906, a year before Kelvin’s death, when Einstein published his famous equation, 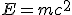 , a consequence of his special theory of relativity. Understanding dawned that the loss of mass was related to a release of energy through the radioactive decay.
, a consequence of his special theory of relativity. Understanding dawned that the loss of mass was related to a release of energy through the radioactive decay.
Our modern knowledge that the sun is powered by nuclear fusion through a process that releases enormous amounts of energy via fusion cycles (interesting, mildly technical paper on its discovery and elucidation) that consume hydrogen atoms to create helium atoms, and then consume those products to produce some heavier elements, was still decades in the future (generally credited to Hans Bethe’s paper published in 1939).
But the message was clear: here was a possible new source of energy for the sun that Kelvin knew nothing about but that could vastly increase the likely age of the Sun.
To finish this part of the story, here is an excerpt from John Gribbin’s The Birth of Time : How Astronomers Measured the Age of the Universe. (New Haven : Yale University Press, 1999. 237 pages.), a fascinating page-turner of a popular science book. (Book note forthcoming.)
If the whole Sun were just slightly radioactive, it could produce the kind of energy that we see emerging from it in the form of heat and light. In 1903, Pierre Curie and his colleague Albert Laborde actually measured the amount of heat released by a gram of radium, and found that it produced enough energy in one hour to raise the temperature of 1.3 grams of water from 0°C to its boiling point. Radium generated enough heat to melt its own weight of ice in an hour–every hour. In July that year, the English astronomer William Wilson pointed out that in that case, if there were just 3.6 grams of radium distributed in each cubic metre of the sun’s volume it would generate enough heat to explain all of the energy being radiated from the Sun’s surface today. It was only later appreciated, as we shall see, that the “enormous energies” referred to by Chamberlin are only unlocked in a tiny region at the heart of the sun, where they produce all of the heat required to sustain the vast bulk of material above them.
The important point, though, is that radioactivity clearly provided a potential source of energy sufficient to explain the energy output of the Sun. In 1903, nobody knew where the energy released by radium (and other radioactive substances) was coming from; but in 1905, another hint at the origin of the energy released in powering both the Sun and radioactive decay came when Albert Einstein published his special theory of relativity, which led to the most famous equation in science, 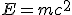 , relating energy and mass (or rather, spelling out that mass is a form of energy.) This is the ultimate source of energy in radioactive decays, where careful measurements of the weights of all the daughter products involved in such processes have now confirmed that the total weight of all the products is always a little less than the weight of the initial radioactive nucleus–the “lost” mass has been converted directly into energy, in line with Einstein’s equation.
, relating energy and mass (or rather, spelling out that mass is a form of energy.) This is the ultimate source of energy in radioactive decays, where careful measurements of the weights of all the daughter products involved in such processes have now confirmed that the total weight of all the products is always a little less than the weight of the initial radioactive nucleus–the “lost” mass has been converted directly into energy, in line with Einstein’s equation.
Even without knowing how a star like the Sun might do the trick of converting mass into energy, you can use Einstein’s equation to calculate how much mass has to be used up in this way every second to keep the Sun shining. Overall, about 5 million tonnes of mass have to be converted into pure energy each second to keep the sun shining. This sounds enormous, and it is, by everyday standards–roughly the equivalent of turning five million large elephants into pure energy every second. But the Sun is so big that it scarcely notices this mass loss. If it has indeed been shining for 4.5 billion years, as the radiometric dating of meteorite samples implies, and if it has been losing mass at this furious rate for all that time, then its overall mass has only diminished by about 4 percent since the Solar System formed.
By 1913, Rutherford was commenting that “at the enormous temperatures of the sun, it appears possible that a process of transformation may take place in ordinary elements analogous to that observed in the well-known radio-elements,” and added, “the time during which the sun may continue to emit heat at the present rate may be much longer than the value computed from ordinary dynamical data [the Kelvin-Helmholtz timescale].” [pp. 36--38]
Kelvin was not always right.
———-
* I’ve taken this image from the Flickr Commons set uploaded by the National Galleries of Scotland, and cropped it some from the original: Source and National Galleries page.
† The history of these ideas in the context of geology as an emerging science is very ably traced in Simon Winchester’s The Map that Changed the World : William Smith and the Birth of Modern Geology (my book note).
Nov
24
Posted by jns on
November 24, 2008
 This is Euclid (c. 365 BCE — c. 275 BCE) of Alexandria, Egypt, possibly one of the earliest celebrities to use only one name. Euclid is famous, of course, for writing Elements, his 13-book exposition on geometry and the earliest mathematical textbook and second only to the Bible in the number of editions published through history.
This is Euclid (c. 365 BCE — c. 275 BCE) of Alexandria, Egypt, possibly one of the earliest celebrities to use only one name. Euclid is famous, of course, for writing Elements, his 13-book exposition on geometry and the earliest mathematical textbook and second only to the Bible in the number of editions published through history.
Invoking Euclid’s name is a ruse. Although there are any number of things related to Euclid and the Elements that we could discuss, what I’ve really been thinking about lately is  , and I needed a pretext. In fact, it wasn’t even exactly
, and I needed a pretext. In fact, it wasn’t even exactly  that I’ve been thinking about so much as people’s relationship with the idea of
that I’ve been thinking about so much as people’s relationship with the idea of  .
.
It’s a trivial thing in a way, but I was perplexed to discover that some googler had reached a small article I had written (“Legislating the Value of Pi“, about the only actual case in history of an attempt to do so–in Indiana) by searching for “accepted value of pi”.
That disturbed me, although I’m finding it difficult to explain why. Let’s talk for a moment about the difference between physical constants and mathematical constants.
In physical theory there are any number of “physical constants”, numbers (with no units) or quantities (with units) that show up in physical theories and are generally presumed to be the same everywhere in the universe and often described as “fundamental” because they can’t be reduced to other other known values. Examples that might be familiar: “c”, the speed of light in a vacuum; “G”, Newton’s universal constant of gravitation; “e”, the charge of the electron; “”h”, Planck’s constant, ubiquitous in quantum mechanics; the list is lengthy. (You can find a long list and a bunch about physical constants at a page maintained by NIST the National Institute of Science and Technology.)
Fundamental physical constants are measured by experiment; that is the only way to establish their value. Some have been measured to extraordinary accuracy, as much as 12 decimal places (or to one part in one-million-million). The NIST website has an “Introduction to the constants for nonexperts“, which you might like to have a look at. (I never quite made it to being a fundamentals-constant experimentalist, but I did do high-precision measurement.)
Now, contrast the ontological status of fundamental constants with mathematical constants, things like “ “, the ratio of the circumference to the diameter of a circle; “e”, the base of the natural logarithms; “
“, the ratio of the circumference to the diameter of a circle; “e”, the base of the natural logarithms; “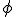 “, the “golden ratio”, and numbers of that ilk. These are numbers that are perfectly well defined by known and exact mathematical relationships. (I once discussed a number of mathematical equations involving “
“, the “golden ratio”, and numbers of that ilk. These are numbers that are perfectly well defined by known and exact mathematical relationships. (I once discussed a number of mathematical equations involving “ ” in “A Big Piece of Pi“.)
” in “A Big Piece of Pi“.)
Now, it may be something odd about the way my mind works (that would be no real surprise), but to me there is a difference in status between fundamental physical constants, which must be measured and will forever be subject to experimental limitations in determining their values, and mathematical constants, which can always be calculated to any desirable precision (number of digits) using exact mathematical expressions.
To me, one can reasonably ask about the “current accepted values” of fundamental physical constants–indeed, you’ll see a similar expression (“adopted values”) on the NIST page–but that “accepted value” makes no sense when used to describe mathematical constants that simply have not been calculated as yet to the precision one might desire. And so, asking about the “accepted value” of  seems like an ill-formed question to me. Your mileage is almost certain to vary, of course.
seems like an ill-formed question to me. Your mileage is almost certain to vary, of course.
Well, now that you’ve made it through that ontological patch of nettles, it’s time for some entertainment. In the aforementioned article I had already discussed some of the fascinating mathematical equations involving  , so we’re just going to have to make do with something a little different, even though it is still an equation involving you know what.
, so we’re just going to have to make do with something a little different, even though it is still an equation involving you know what.
The problem of “Buffon’s Needle” was first put forward in the 18th century by Georges-Louis Leclerc, Comte de Buffon. I like the way Wikipedia states it (or find another discussion here):
Suppose we have a floor made of parallel strips of wood, each the same width, and we drop a needle [whose length is the same as the width of the strips of wood] onto the floor. What is the probability that the needle will lie across a line between two strips?
Worked it out yet?
You can always measure an approximate value of the probability for yourself with a needle and a sheet of paper on which you have ruled parallel lines separated by the length of the needle. Drop the needle on the paper a whole bunch of times. Divide the number of times the needle lands on a line by the total number of times you dropped the needle. What value do you get closer to the more times you do the drop the needle?
The answer: 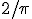 . Exactly.
. Exactly.
 I did not plan to become the expert on such an arcane topic–although I can answer the question as it arises–but once I had written a blog posting called “
I did not plan to become the expert on such an arcane topic–although I can answer the question as it arises–but once I had written a blog posting called “ This is the youthful Galileo Galilei (1564–1642), who established the intellectual starting point for this short discussion.
This is the youthful Galileo Galilei (1564–1642), who established the intellectual starting point for this short discussion. This is* author John R. Gribbin (1946– ), a science writer who started life as an astrophysicist. (
This is* author John R. Gribbin (1946– ), a science writer who started life as an astrophysicist. ( This* is Scottish physicist James Clerk Maxwell (1831–1879). He did significant work in several fields (including statistical physics and thermodynamics, in which I used to research) but his fame is associated with his electromagnetic theory. Electromagnetism combined the phenomena of electricity and magnetism into one, unified field theory. Unified field theories are still all the rage. It was a monumental achievement, but there was also a hidden bonus in the equations. We’ll get to that.
This* is Scottish physicist James Clerk Maxwell (1831–1879). He did significant work in several fields (including statistical physics and thermodynamics, in which I used to research) but his fame is associated with his electromagnetic theory. Electromagnetism combined the phenomena of electricity and magnetism into one, unified field theory. Unified field theories are still all the rage. It was a monumental achievement, but there was also a hidden bonus in the equations. We’ll get to that.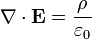
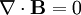
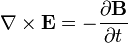
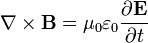
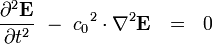
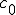 , which is related to the product of the physical constants
, which is related to the product of the physical constants  and
and 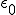 that appeared in the earlier equations.
that appeared in the earlier equations.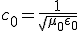
 This is physicist and science-fiction author Gregory Benford. His
This is physicist and science-fiction author Gregory Benford. His 

 This is Sir William Thomson, Baron Kelvin* (1824 – 1907) or, simply, Lord Kelvin as he’s known to us in the physical sciences. This is the same “Kelvin” as in the SI unit “Kelvins”, the degrees of the absolute thermodynamic temperature scale.
This is Sir William Thomson, Baron Kelvin* (1824 – 1907) or, simply, Lord Kelvin as he’s known to us in the physical sciences. This is the same “Kelvin” as in the SI unit “Kelvins”, the degrees of the absolute thermodynamic temperature scale.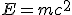 , a consequence of his special theory of relativity. Understanding dawned that the loss of mass was related to a release of energy through the radioactive decay.
, a consequence of his special theory of relativity. Understanding dawned that the loss of mass was related to a release of energy through the radioactive decay. This is Euclid (c. 365 BCE — c. 275 BCE) of Alexandria, Egypt, possibly one of the earliest celebrities to use only one name. Euclid is famous, of course, for writing Elements, his 13-book exposition on geometry and the earliest mathematical textbook and second only to the Bible in the number of editions published through history.
This is Euclid (c. 365 BCE — c. 275 BCE) of Alexandria, Egypt, possibly one of the earliest celebrities to use only one name. Euclid is famous, of course, for writing Elements, his 13-book exposition on geometry and the earliest mathematical textbook and second only to the Bible in the number of editions published through history. , and I needed a pretext. In fact, it wasn’t even exactly
, and I needed a pretext. In fact, it wasn’t even exactly 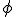 “, the “golden ratio”, and numbers of that ilk. These are numbers that are perfectly well defined by known and exact mathematical relationships. (I once discussed a number of mathematical equations involving “
“, the “golden ratio”, and numbers of that ilk. These are numbers that are perfectly well defined by known and exact mathematical relationships. (I once discussed a number of mathematical equations involving “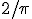 . Exactly.
. Exactly.