Archive for the ‘Ideas’ Category
Feb
03
Posted by jns on
February 3, 2010
A long-time friend of mine, quite inadvertently and perhaps to his lasting regret, brought up the subject of special relativity : we briefly touched on the idea central to special relativity that the speed of light (in vacuum) is constant (as measured) in every inertial reference frame.*
At first hearing it’s a rather unsettling idea, and of course one wonders how one could possibly make a physical theory around such an idea and have it come out in any meaningful way. Well, one can if one is Einstein, and there are unexpected and startling consequences that flow logically from that simple idea about the speed of light.
The next step in our conversation–not surprising since I was party to the discussion–was “what book should one read to learn these things about special relativity?”
Well, that turned out a bit of a poser. I was certain that we should have something appropriate in our Scienticity Book Notes collection, but there was nothing. Nothing at all!
Well, that was a deficiency that needed some attention. So, we need to have some books read about special relativity and some notes written. Therefore, I’ve put together a tentative wish list of titles that look promising.
I say “promising”–there are no guarantees. Everyone who writes a book on a subject has unique ideas about what should be discussed and how to go about it, and I’ll admit that not all of those ideas align with my ideas about what should be in the book.
I’d like a book about light — not about vision, or color, or art, or optics, but light itself, what it is, how we think about it now, how we used to think about it, how unusual is its place in the physical universe, and then about how the idea of the constancy of the speed of light (in vacuum, in inertial frames, etc.) lies at the heart of special relativity (which is a theory of “electrodynamics”, i.e., a theory of moving charged particles and interactions with electromagnetic fields, i.e.2, essentially a theory of light).
I don’t think the readers I have in mind are much interested in deriving mathematical consequences and such, so there needn’t be a go at developing, say, the Lorentz-contraction equations, but the concepts and ideas must be explored for the average reader in a nonpatronizing way.
It may be too tall an order. I’d just as soon not write the book myself at this time, although it would make a fabulous subject if it’s not been written. (Please let me know if you personally know of such a book.)
And so, the following reading list, the result of a rather cursory look at some sources to try to uncover some candidate titles.
- Brian Cox, Why Does E=mc2?: And Why Should We Care? (Powell’s synopsis). I’m not so interested in the “deeper” meaning of that famous equation — it’s really far from the most important idea of special relativity despite it’s explosive significance — but the synopsis suggested that Cox might explore the ideas in a useful way.
- Richard P. Feynman, Six Not So Easy Pieces: Einstein’s Relativity, Symmetry, & Space-Time (Powell’s synopsis). I know, even Feynman’s “Easy Pieces” are far from easy, but if one is in the mood to read slowly and savor, there’s a high density of delight in Feynman’s expositions, and I’d like to know just how hard these seem to normal people.
- Alan Lightman, Great Ideas in Physics (Powell’s synopsis). This book isn’t exclusively about light or relativity, but the few other books I’ve read by Lightman were very nicely written and he impressed me with with profound understanding of the ideas he talks about, so it made this list with high hopes.
- N. David Mermin, It’s about Time: Understanding Einstein’s Relativity (Powell’s synopsis). I knew Mermin’s name during my years as a working physicist from his writing, which I regarded highly. This apparently is his attempt to do just what I would like to see done, so I’m keenly interested in the result.
- Nigel Calder, Einstein’s Universe : a Guide To the Theory of Relativity (79 Edition) (Powell’s synopsis). When I was a young pre-scientist, Calder had quite a reputation as a popularizer, but I’ve never read any of his writing so I can’t comment. Maybe this is the jewel we seek?
If you know about these, or have other titles to suggest, please chime in.
If you’d like to read and write about some of them as part of your Science-Book Challenge (What, not already signed up? Tsk. Use that link and do it now!), that would be fabulous and will help other people when the question comes up again, as it most certainly will.
———-
*You can take this to mean any frame of reference, i.e., viewpoint, that is moving at a constant velocity, i.e, not accelerated; accelerated frames of reference are the subject of general relativity (Einstein’s theory of gravitation). If you’d like to know more about this idea of reference frames, I can recommend the now vintage but very fine film “Frames of Reference”, which you will find as the second video offering in this blog posting of mine.
Sep
07
Posted by jns on
September 7, 2009
 This is Congressman John Fletcher Lacey (1841 – 1913).* Mr. Lacey came to my attention while I was writing a short article on the introduction of starlings to North America (“Starlings Arrive in North America“), of all things. Just how his name came up should become clear shortly.
This is Congressman John Fletcher Lacey (1841 – 1913).* Mr. Lacey came to my attention while I was writing a short article on the introduction of starlings to North America (“Starlings Arrive in North America“), of all things. Just how his name came up should become clear shortly.
Here is my abridged version of his official biography (Biographical Directory of the United States Congress):
Representative from Iowa; born in New Martinsville, Va. (now West Virginia), May 30, 1841; moved to Iowa in 1855 with his parents, who settled in Oskaloosa; attended the common schools and pursued classical studies; engaged in agricultural pursuits; learned the trades of bricklaying and plastering; enlisted in Company H, Third Regiment, Iowa Volunteer Infantry, in May 1861[; ...] studied law; was admitted to the bar in 1865 and commenced practice in Oskaloosa, Iowa; [...] elected as a Republican to the Fifty-first Congress (March 4, 1889-March 3, 1891); unsuccessful candidate for reelection; elected to the Fifty-third and to the six succeeding Congresses (March 4, 1893-March 3, 1907); chairman, Committee on Public Lands (Fifty-fourth through Fifty-ninth Congresses); was an unsuccessful candidate for reelection; resumed the practice of law; died in Oskaloosa, Iowa, September 29, 1913….
These days we’d find it exceedingly odd to find the name of someone associated with the Republican party to be a leading conservationist, but times have changed and Lacey is remembered for two important legislative innovations in conservation: “The Lacey Act of 1900″, and “The Antiquities Act of 1906″.
“The Lacey Act of 1900“, sponsored by the congressman, was “the first Federal law protecting game, prohibiting the interstate shipment of illegally taken wildlife, as well as the importation of injurious species. Enforcement of this Act became the responsibility of the Division of Biological Survey, U.S. Department of Agriculture.” (source) The ban on the importation of “injurious species” was the connection with starlings and their introduction to North America, although the legislation came 10 years too late to halt that process.
A curious article from the Thoreau Institute (“State Fish & Wildlife Agencies“) gives some background to the Lacey Act:
A legal tradition dating back thousands of years governed wildlife by a “rule of capture”–meaning that they are owned by no one unless killed or captured. Under U.S. common law, wildlife are owned by the people, and the states, rather than federal or local governments, have jurisdiction over their use.
Therefore, regulation of “market hunting” was up to the states. Some few did regulate the practice in the late 1800s, but most did not. This resulted in the common evasive practice of animals being killed illegally in one state and transported into another, where killing them was legal, for sale.
Efforts to ban or regulate commercial hunting accelerated in 1887 when Theodore Roosevelt and George Bird Grinnell started the Boone and Crockett Club, which soon became the most powerful conservation organization in the country. The club is not as well known today, partly because it restricts its membership to 100 people, but those 100 people tend to be highly influential.
Bans on commercial hunting were difficult to enforce when hunters could take their wares across state lines. In 1900, Boone and Crockett Club member and Iowa Congressman John Lacey convinced Congress to pass a federal law prohibiting interstate shipping of wildlife taken in violation of a state game law. This effectively put commercial hunters out of business.
The Lacey Act was signed into law on May 25, 1900 by President William McKinley.
By the time Lacey introduced “The Antiquities Act of 1906“, Congress had already been creating national parks for some 40 years, including Yosemite Valley, Yellowstone National Park, General Grant, Sequoia, Mount Ranier, and Casa Grande and Mesa Verde. (source). It was concern about vandalism and theft of antiquities from the two historic Indian sites that prompted the Antiquities Act. The bill, signed into law by Theodore Roosevelt on June 8, 1906, gave the President authority to restrict the use of particular public land owned by the federal government by using an executive order to designate a “national monument”. The first use of the act: Roosevelt proclaimed Devils Tower National Monument, Wyoming, on September 24, 1906. (source)
While I was researching Congressman Lacey’s contributions I came across one more interesting one worth noting, this having to do with the “Jefferson Bible”. You may recall that this refers to Thomas Jefferson’s highly abridged version of the New Testament in which he cut out all the miraculous and mystical stuff he didn’t care for and kept the better ethical teachings of Jesus, ending up with a slim, svelt 82-page volume. The work has been published on several occasions, notably the Beacon Press, associated with the Unitarian Church.
Here reporter Cathrine Dunn (“Jefferson Bible returns to publication“) takes up the story:
In 1886 Cyrus Adler found the book, which had been passed down through the Jefferson family. He bought the original copy and donated it to the National Museum – now the Smithsonian Institution – where Iowa Congressman John Lacey happened upon it at the turn of the century [i.e., c1900].
It was Lacey who initiated the idea of publishing the book, introducing legislation in Congress that would fund the printing and distribution of the Jefferson Bible to all senators and representatives at the start of their terms.
Lacey saw the book as an important “moral basis for representatives,” said Bellevue University economics professor Judd Patton. “For a good government, we need to have good leaders with moral principles.”
For unknown reasons the Government Printing Office stopped publishing the book in 1957, and its distribution to new congressional members ceased.
———-
* Image source: collection National Conservation Training Center, U.S. Fish & Wildlife Service.
Aug
11
Posted by jns on
August 11, 2008

This is Georg Cantor (1845–1918), the German mathematician who advanced set theory into the infinite with his discovery/invention of transfinite arithmetic. Why I hedge over “discovery” or “invention” we’ll get to in a moment.
I first encountered Cantor’s ideas in college in my course of “mathematical analysis”, which was largely concerned with number theory. I remember the stuff we worked on as beautiful but nearly inscrutable, and very dense: our textbook was less than an inch thick but the pages were dark with mathematical symbols, abbreviations, and shorthand, so that a semester was much too short a time to get through the whole thing.
Cantor proved a series of amazing things. First, consider the positive integers (or natural numbers, or whole numbers, or counting numbers): 1, 2, 3, 4, etc. We know that there is no largest integer because, if there were, we could add 1 to it to get one larger. Therefore, the set of positive whole numbers is infinite. This is also described as a countable, or denumerable infinity, because the elements of the set can be put into a one-to-one correspondence with the counting numbers–a rather obvious result because they are the counting numbers and can thus be counted. Think of counting and one-to-one correspondence for a bit and is becomes obvious (as the textbooks are wont to say) that the set of positive and negative integers (…,-3, -2, -1, 0, 1, 2, 3, …) is also a countable infinity, i.e., there are just as many positive and negative integers as there are positive ones. (This is transfinite arithmetic we’re talking about here, so stay alert.)
Next to consider is the infinity of rational numbers, or those numbers that can be written as the ratio of two whole numbers, i.e., fractions. How infinite are they compared to the whole numbers?
Cantor proved that the cardinality of the rational numbers is the same as that of the whole numbers, that the rational numbers are also denumerable. For his proof he constructed a system of one-to-one correspondence between the whole numbers and the rationals by showing how all of the rational numbers (fractions) could be put into an order and, hence, counted. (The illustration at the top of this page shows how the rationals can be ordered without leaving any out.)
Any set whose elements can be put into a one-to-one correspondence with the whole numbers, i.e., that can be counted, contains a countable infinity of elements. Cantor gave a symbol to this size, or cardinality, or infinity, calling it 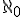 (said “aleph nought”), using the first letter of the Hebrew alphabet, named “aleph”.
(said “aleph nought”), using the first letter of the Hebrew alphabet, named “aleph”.
Then there are the irrational numbers, numbers that cannot be written as ratios of whole numbers. The square root of 2 is a famous example; discovery of its irrationality is said to have caused great consternation among Pythagoreans in ancient times. There are several interesting classes of irrational numbers, but for this consideration it is enough to say that irrational numbers have decimal expansions that never terminate and whose digits never repeat.  , the ratio of the circumference to the diameter of a circle is a famous irrational number and many people are fascinated by its never ending decimal representation.
, the ratio of the circumference to the diameter of a circle is a famous irrational number and many people are fascinated by its never ending decimal representation.
Cantor proved that the cardinality of the real numbers (rational and irrationals put together) is greater than 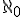 — they cannot be counted. He proved this with his diagonalization technique, in which he showed that no matter how many rational numbers were packed into an interval one more could always be constructed that was not in that set.* (For the proof, see this Wikipedia page; it’s not a difficult proof to read but it takes a clear head to understand it.)
— they cannot be counted. He proved this with his diagonalization technique, in which he showed that no matter how many rational numbers were packed into an interval one more could always be constructed that was not in that set.* (For the proof, see this Wikipedia page; it’s not a difficult proof to read but it takes a clear head to understand it.)
Cantor referred to the real numbers as the continuum because it was so dense with numbers. Cantor had shown that the cardinality of the continuum was strictly larger than the cardinality of the whole numbers. Now we have two sizes of infinity, if you will! There are more, but we’ll stop there.
Cantor was haunted by being unable to prove something he believed to be true, known as the “continuum hypothesis”. In words the conjecture is that there is no cardinality of infinity between the cardinality of the countable infinity and the cardinality of the real numbers. When he’d reached this stage Cantor’s mental health faced severe challenges and he became obsessed with trying to prove that Francis Bacon wrote the plays of Shakespeare. A decade after Cantor died Kurt Gödel proved that the Continuum Hypothesis was a formally undecidable proposition of set theory, that it could neither be proved or disproved.
Much of this story appeared in one book I finished recently: Amir D Aczel, The Mystery of the Aleph : Mathematics, the Kabbalah, and the Search for Infinity (New York : Four Walls Eight Windows, 2000, 258 pages). My book note is here.
Just after that book I finished another book on a mathematical topic: Mario Livio, The Golden Ratio : The Story of Phi, The World’s Most Astonishing Number (New York : Broadway Books, 2002, viii + 294 pages). Its book note is here.
Aside from their interest in mathematical topics, the two books have very little in common with one exception: both authors ruminated on the question whether mathematics is created or discovered, whether the great edifice exists only in the minds of humans or whether it somehow has an independent existence in the universe independent of the human mind. The complication to the question of course is the remarkable utility of mathematics when it comes to explaining how the universe works.
I once had a long-time debate with my roommate in graduate school on the question. I remember winning the debate after months, but I forget which side I argued. It’s the sort of thing that physics and philosophy graduate students argue about.
Oddly to me, aside from the vague coincidence that two books I should read back-to-back considered this question,† is that each author felt very strongly about the answer to the question, feeling that his answer was the obvious best choice, but, as you’ve guessed, one believed that mathematics was obviously discovered and the other felt that mathematics was clearly invented.
Even as I once argued that mathematics was obviously discovered, I realized from reading these two authors’ discussions that I now pretty much would go with the conclusion that mathematics is an invention of the human mind. Now, how that could be and still have mathematics accord so well with the operating of the universe is a question that I’m afraid goes well beyond the scope of this already too long posting.
Besides, the hour grows late and my mind lacks the clarity to be convincing right now. So, as a distraction, I leave you thinking about the much simpler question of how one type of infinity can be larger than another.
__________
* Think very carefully about the distinction between not being able to think of a way to count the set versus proving that there is no way it can be done.
† Not so surprising, really, if you consider the fact that when I’m browsing for books on the library stacks I’ll frequently find more than one on a single shelf that looks interesting.
 This is Congressman John Fletcher Lacey (1841 – 1913).* Mr. Lacey came to my attention while I was writing a short article on the introduction of starlings to North America (“
This is Congressman John Fletcher Lacey (1841 – 1913).* Mr. Lacey came to my attention while I was writing a short article on the introduction of starlings to North America (“
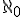 (said “aleph nought”), using the first letter of the Hebrew alphabet, named “aleph”.
(said “aleph nought”), using the first letter of the Hebrew alphabet, named “aleph”. , the ratio of the circumference to the diameter of a circle is a famous irrational number and many people are fascinated by its never ending decimal representation.
, the ratio of the circumference to the diameter of a circle is a famous irrational number and many people are fascinated by its never ending decimal representation.