Infinity and Beyond

Posted by jns on 11 August 2008

This is Georg Cantor (1845–1918), the German mathematician who advanced set theory into the infinite with his discovery/invention of transfinite arithmetic. Why I hedge over “discovery” or “invention” we’ll get to in a moment.

I first encountered Cantor’s ideas in college in my course of “mathematical analysis”, which was largely concerned with number theory. I remember the stuff we worked on as beautiful but nearly inscrutable, and very dense: our textbook was less than an inch thick but the pages were dark with mathematical symbols, abbreviations, and shorthand, so that a semester was much too short a time to get through the whole thing.

Cantor proved a series of amazing things. First, consider the positive integers (or natural numbers, or whole numbers, or counting numbers): 1, 2, 3, 4, etc. We know that there is no largest integer because, if there were, we could add 1 to it to get one larger. Therefore, the set of positive whole numbers is infinite. This is also described as a countable, or denumerable infinity, because the elements of the set can be put into a one-to-one correspondence with the counting numbers–a rather obvious result because they are the counting numbers and can thus be counted. Think of counting and one-to-one correspondence for a bit and is becomes obvious (as the textbooks are wont to say) that the set of positive and negative integers (…,-3, -2, -1, 0, 1, 2, 3, …) is also a countable infinity, i.e., there are just as many positive and negative integers as there are positive ones. (This is transfinite arithmetic we’re talking about here, so stay alert.)

Next to consider is the infinity of rational numbers, or those numbers that can be written as the ratio of two whole numbers, i.e., fractions. How infinite are they compared to the whole numbers?

Cantor proved that the cardinality of the rational numbers is the same as that of the whole numbers, that the rational numbers are also denumerable. For his proof he constructed a system of one-to-one correspondence between the whole numbers and the rationals by showing how all of the rational numbers (fractions) could be put into an order and, hence, counted. (The illustration at the top of this page shows how the rationals can be ordered without leaving any out.)

Any set whose elements can be put into a one-to-one correspondence with the whole numbers, i.e., that can be counted, contains a countable infinity of elements. Cantor gave a symbol to this size, or cardinality, or infinity, calling it 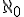(said “aleph nought”), using the first letter of the Hebrew alphabet, named “aleph”.

Then there are the irrational numbers, numbers that cannot be written as ratios of whole numbers. The square root of 2 is a famous example; discovery of its irrationality is said to have caused great consternation among Pythagoreans in ancient times. There are several interesting classes of irrational numbers, but for this consideration it is enough to say that irrational numbers have decimal expansions that never terminate and whose digits never repeat. , the ratio of the circumference to the diameter of a circle is a famous irrational number and many people are fascinated by its never ending decimal representation.

Cantor proved that the cardinality of the real numbers (rational and irrationals put together) is greater than 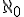— they cannot be counted. He proved this with his diagonalization technique, in which he showed that no matter how many rational numbers were packed into an interval one more could always be constructed that was not in that set.^* (For the proof, see this Wikipedia page; it’s not a difficult proof to read but it takes a clear head to understand it.)

Cantor referred to the real numbers as the continuum because it was so dense with numbers. Cantor had shown that the cardinality of the continuum was strictly larger than the cardinality of the whole numbers. Now we have two sizes of infinity, if you will! There are more, but we’ll stop there.

Cantor was haunted by being unable to prove something he believed to be true, known as the “continuum hypothesis”. In words the conjecture is that there is no cardinality of infinity between the cardinality of the countable infinity and the cardinality of the real numbers. When he’d reached this stage Cantor’s mental health faced severe challenges and he became obsessed with trying to prove that Francis Bacon wrote the plays of Shakespeare. A decade after Cantor died Kurt Gödel proved that the Continuum Hypothesis was a formally undecidable proposition of set theory, that it could neither be proved or disproved.

Much of this story appeared in one book I finished recently: Amir D Aczel, The Mystery of the Aleph : Mathematics, the Kabbalah, and the Search for Infinity (New York : Four Walls Eight Windows, 2000, 258 pages). My book note is here.

Just after that book I finished another book on a mathematical topic: Mario Livio, The Golden Ratio : The Story of Phi, The World’s Most Astonishing Number (New York : Broadway Books, 2002, viii + 294 pages). Its book note is here.

Aside from their interest in mathematical topics, the two books have very little in common with one exception: both authors ruminated on the question whether mathematics is created or discovered, whether the great edifice exists only in the minds of humans or whether it somehow has an independent existence in the universe independent of the human mind. The complication to the question of course is the remarkable utility of mathematics when it comes to explaining how the universe works.

I once had a long-time debate with my roommate in graduate school on the question. I remember winning the debate after months, but I forget which side I argued. It’s the sort of thing that physics and philosophy graduate students argue about.

Oddly to me, aside from the vague coincidence that two books I should read back-to-back considered this question,^† is that each author felt very strongly about the answer to the question, feeling that his answer was the obvious best choice, but, as you’ve guessed, one believed that mathematics was obviously discovered and the other felt that mathematics was clearly invented.

Even as I once argued that mathematics was obviously discovered, I realized from reading these two authors’ discussions that I now pretty much would go with the conclusion that mathematics is an invention of the human mind. Now, how that could be and still have mathematics accord so well with the operating of the universe is a question that I’m afraid goes well beyond the scope of this already too long posting.

Besides, the hour grows late and my mind lacks the clarity to be convincing right now. So, as a distraction, I leave you thinking about the much simpler question of how one type of infinity can be larger than another.
__________
^* Think very carefully about the distinction between not being able to think of a way to count the set versus proving that there is no way it can be done.

^† Not so surprising, really, if you consider the fact that when I’m browsing for books on the library stacks I’ll frequently find more than one on a single shelf that looks interesting.