Archive for the ‘Explaining Things’ Category
Dec
30
Posted by jns on
December 30, 2007
Isaac & I returned home yesterday, flying from Kansas City (central standard time) to Washington, DC (eastern standard time). As we arrived at the gate in DC, I overheard this conversational exchange from the seats in front of mine:
Mother: Oh, look! My cell phone has changed back to eastern time.
Teen-age son: That’s because they work with satellites, and they know where you are.
I was a bit surprised that, contrary to common belief, young people still don’t know everything. There is at least one surprising misconception in the son’s mind that I should have cleared up on the spot, but I didn’t. Y’all are so lucky.
Modern mobile phones, known also as cell phones, do not communicate through satellites, and they never have. There have existed satellite telephones that do, but they’re a much different beast, not to mention much larger and much heavier.
Cell phones communicate with cell towers–or, more generally, cell sites, since not all cellular antennae are on towers; many are hidden on building tops, for instance. If the cell sites are visible they are easily recognizable, most often triangular structures with vertical “bars” on each face of the triangle. Each of the “bars” is actually an antenna for transmitting to mobile phones or else receiving signals from them. The antennae are used in pairs so that they send and receive signals directionally.
The whole idea of “cells” was originally the way to provide coverage over a wide area without requiring a large amount of power in the handset, and also as a way to use restricted amounts of radio-frequency bandwidth efficiently and provide for a number of users.
In some area over which the cellular provider wants coverage, the area is divided into hexagonal “cells” that cover the area. (Look at a bathroom floor sometime that has 6-sided tiles and you will see that the area can be completely covered without gaps.) At the center of each cell is a cell site. The cell site has the three-sided shape so that it can hear in all directions. A cell site is responsible for all the cellular phones in its cell.
The imagined boundaries of the cells overlap a bit, so each cell actually operates on a slightly different frequency# from all of its neighbors. Because of that, cell sites over a wider area can reuse frequencies, but there is the added technical challenge of tracking a particular cell phone between the ranges of neighboring cell sites and switching an active conversation from being routed through one cell site to being routed to another without dropping the call. That process is call “handover”. When a particular phone switches cells it also shifts the frequency that it uses for the radio link by a small amount.
The size of each cell varies depending on terrain and obstructions and such things, but in denser areas cell sites will be about 5 to 8 miles apart, so that’s the furthest that you cell phone usually has to transmit its signal, which is something it can manage to do with the relatively tiny batteries that it carries.
Cell sites do not continuously track a cell phone unless the phone is engaged in a conversation. If your phone has been off, it will always talk with the nearest cell site when you turn it back on and the phone network takes note of your position. Occasionally every cell sites will query phones with broadcast messages; the phones respond, and that way your cellular network can quickly find which cell site to use to contact your phone when you are receiving a call. The cell sites also broadcast timing signals, which is how cell phones always seem to know the right time. Note this: the cell site doesn’t have to know where your phone is to get the time correct, instead your phone simply takes the local time of the cell site that it can hear.
Now, one last note about cell phones talking through satellites. Most communications satellites are in geostationary orbits, which means they are in orbits where they appear stationary in the sky. This is where you will find the satellites that broadcast satellite radio and television, too.
Anyway, to be in a geosynchronous orbit requires that the satellite be at an altitude of about 22,000 miles. That’s a long way compared to the 8-mile distance to the nearest cell site. In fact, it’s about 2,750 times as far away. Other things being equal* that means that the cell phone would require 7.6 million times the power for its signal to reach the satellite. As you might guess, the would require a much bigger battery than your cell phone has in it.
By the way, before I finish, I have to chastise the FCC for poor technical writing. I was looking around for a few details about cell-phone networks and I found this page of “Cell Phones FAQs” from “The FCC Kids [sic] Zone”. You may wish to look at the answer for “How Does a Cell Phone Work” and count how many errors and imprecise statements you can find in one paragraph. (For extra credit, read the other answers if you can stand it.) There are many irritants, but I could start with the absurdity of using the copper-wire based, home phone system as a conceptual basis, since kids don’t use that archaic communication system anymore as a conceptual referent.
There there’s this statement:
A cell phone turns your voice into a special type of electricity and sends it over the air to a nearby cell tower; the tower sends your voice to the person you are calling.
Calling propagating electromagnetic waves a “special type of electricity” is incorrect and unnecessary, an egregious error. Saying the tower “sends your voice” is no better. Despite what this FCC author seemed to think, it’s entirely possible not to go into pages of detail about the time-slice multiplexing and analog-signal digitization (most cell networks these days are digital) used to “send your voice” over the network and still get it right without the stupid and inaccurate “send your voice” gambit.
These are just the type of gratuitous and imprecise over-simplifications about science and technology that drive me into a frenzy and that I have vowed that Ars Hermeneutica will combat. If any of my four regular readers happen to know someone at the FCC, have them get in touch and we can straighten out these things before any more bad ideas get into kids’ (note the apostrophe) heads.
———-
# Cell phones also use a different frequency to transmit from the frequency they use for receive, but that’s a needless conceptual complication at this stage.
* There are details, naturally. The 7.6 million number is the square of 2,750, because radiated electromagnetic power diminishes as the square of the distance. However, satellite communications is possible with these geosynchronous satellites because their receivers have much higher gain (i.e., can hear much weaker signals) than terrestrial cell sites. They also are much too far away to be able to break an urban region up into cells and distinguish calls from different cells, let alone transmit in different cells, but that’s a whole other story.
Oct
24
Posted by jns on
October 24, 2007
Bubbles seem to be on the net’s mind today. I haven’t kept all the references (here’s one: “Scientists map near-Earth space bubbles“) but it seemed that I kept reading things involving bubbles.
Now, I’ve long been fascinated by bubbles although, despite my being a scientist with a history of doing some hydrodynamics and a relatively keen interest in things dealing with buoyancy, I’ve never worked on bubbles. This is odd, because I’ve long had a question about bubbles that I’ve never answered — probably because I never spent any time thinking about it. Now, apparently, I have to give it some thought.
My question is not particularly well formed, which makes it not a terribly good scientific question.* Nevertheless, I’ve always wondered what it is that determines the bubble size in effervescent drinks. In all classes of drinks with bubbles — soda, beer, champagne, effervescent water — there are those that have smaller bubbles and those that have larger bubbles. As a rule, I tend to prefer smaller bubbles, by the way.
The last time this question crossed my mind and there were people around who might agreeably talk about the issue, we talked about it but came to no conclusion. I think our problem was that we were imagining that it was the effect of bottle size or the shape of a bottle’s neck or some similar incidental phenomenon that determined bottle size, otherwise assuming that all carbonated beverages were otherwise equal. It now seems to me that making that assumption was rather naive and silly.
My thought today is that the bubble size is determined locally in the fluid, that is to say by the physical-chemical environment in the immediate vicinity of the bubble.# It seems to me that there are two questions to consider on our way to the answer:
- Why do bubbles grow?
- Why would a bubble stop growing?
The answer to the second question, of course, might be implicit in the answer to the first.
To begin: what is a bubble? Bubbles happen in mixtures of two or more substances when little pockets of stuff-B collect inside predominantly stuff-B. That means there’s a lot more of stuff-A than stuff-A, which is to say that we usually see bubbles of stuff-B when there’s only a little bit of stuff-B mixed in with a whole bunch of stuff-A.
To be concrete, let’s talk about bubbles of carbon-dioxide (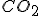 ) in effervescent water, say “San Benedetto” brand.% Now, bubbles have very few features of any physical importance: their sizeis an important one, and the interface between the inside and outside of the bubble, which we might call the surface of the bubble. Some chemical properties of the stuff inside and outside the bubble might matter, too, but let’s save that for a moment.
) in effervescent water, say “San Benedetto” brand.% Now, bubbles have very few features of any physical importance: their sizeis an important one, and the interface between the inside and outside of the bubble, which we might call the surface of the bubble. Some chemical properties of the stuff inside and outside the bubble might matter, too, but let’s save that for a moment.
Now, imagine that we start observing through our clear-glass bottle of San Benedetto water before we take the cap off. The water is clear and there are no bubbles. However, we are aware that there is 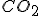 dissolved in the water. In fact, we know that (in some sense) the
dissolved in the water. In fact, we know that (in some sense) the 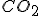 is under pressure because, when we unscrew the cap, we hear a “pffft” sound. Not only that, bubbles instantly appear and float up to the surface of the water, where they explode and make little “plip plip plip” sounds.
is under pressure because, when we unscrew the cap, we hear a “pffft” sound. Not only that, bubbles instantly appear and float up to the surface of the water, where they explode and make little “plip plip plip” sounds.
What makes the bubbles grow? They start out as microscopically tiny things,** gradually grow bigger, until they are big enough to float to the top of the bottle and explode.
To be more precise, bubbles of 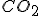 grow if it takes less energy to let a molecule into the bubble across its surface than it costs to keep it outside the bubble. (This is a physicist’s way of looking at the problem, to describe it in terms of the energy costs. A chemist might talk about it differently, but we end up describing the same things.)
grow if it takes less energy to let a molecule into the bubble across its surface than it costs to keep it outside the bubble. (This is a physicist’s way of looking at the problem, to describe it in terms of the energy costs. A chemist might talk about it differently, but we end up describing the same things.)
What causes the bubble to float up? That’s a property called buoyancy, the name of the pseudo-force that makes things float. It’s determined by the relative density of the two substances: less dense stuff floats up, more dense stuff floats down. Notice that the use of “up” and “down” requires that we have gravity around — there is no buoyancy in orbit around the Earth, for instance.
Bubbles, then, will start to float up when they get big enough that they have enough buoyancy to overcome the forces that are holding them in place. That basically means overcoming drag produced by the water’s viscosity, which works kind of like friction on the bubble — but that’s a whole other story, too.
Are we near the answer about bubble size yet? Well, here’s one possibility: bubbles grow until they are big enough to float up to the surface and pop, so maybe they don’t get bigger because they shoot up and explode before they have the chance.
I don’t like that answer for a few reasons. We began by observing that different brand products had different size bubbles, meaning different size bubbles exploding at the surface, so something is going on besides the simple matter of 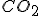 dissolved in water, or else they would all have the same size bubbles. You can look at the bubbles floating up from the bottom and see that they are different sizes in different products to begin with and they don’t change size much on the way up. Thus: bubbles grow very quickly to their final size and their size does not seem limited by how it takes them to float up. Another reason: sometimes bubbles get stuck to the sides of the bottle, but they don’t sit there and grow to arbitrary sizes; instead, they tend to look much like the freely floating bubbles in size.
dissolved in water, or else they would all have the same size bubbles. You can look at the bubbles floating up from the bottom and see that they are different sizes in different products to begin with and they don’t change size much on the way up. Thus: bubbles grow very quickly to their final size and their size does not seem limited by how it takes them to float up. Another reason: sometimes bubbles get stuck to the sides of the bottle, but they don’t sit there and grow to arbitrary sizes; instead, they tend to look much like the freely floating bubbles in size.
There could be a chemical difference, with different substances in the drink limiting the size of the bubbles for some chemical reason. Certainly that’s a possibility, but it’s not what I’m interested in here because I want to explain how there can be bubbles of such obviously different sizes in different brands of what is pretty basically water with insignificant chemical differences in their impurities.
That seems to leave us with one option: the energy balance between the inside and outside of the bubble. Whatever it was that caused it to be favorable for dissolved 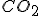 to rush into the bubble at first has some limit. There is some reason that once the bubble reaches a particular size, the energy balance no longer favors
to rush into the bubble at first has some limit. There is some reason that once the bubble reaches a particular size, the energy balance no longer favors 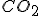 crossing preferentially from water to bubble interior and the bubble stops growing.
crossing preferentially from water to bubble interior and the bubble stops growing.
Now we can look at the “energy balance” matter a little more closely. There are two forces at work. One is osmotic pressure. Osmosis describes how stuff-A moves relative to stuff-B across a barrier (in this case the surface of the bubble); osmotic pressure is the apparent force that causes one substance to move relative to the other across the interface.
The forces at work keeping the bubble in shape are two. One is osmotic pressure inside the bubble, where there is a significantly higher concentration of 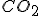 than in the fluid outside, so it creates an outward pressure at the bubble’s surface. The other is the pressure of the water on the surface of the bubble, trying to keep it from expanding.
than in the fluid outside, so it creates an outward pressure at the bubble’s surface. The other is the pressure of the water on the surface of the bubble, trying to keep it from expanding.
So, it looks like the size of the bubbles are determined by a balance between water pressure –determined by the water’s density and gravity — and osmotic pressure inside the bubble, which is caused by the relative concentrations of 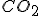 inside and outside the bubble.
inside and outside the bubble.
It would seem, then, that bubbles grow in size until the water pressure on the bubble, which is trying to squeeze it smaller, matches the osmotic pressure of the 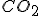 inside the bubble, which is trying to expand the bubble.
inside the bubble, which is trying to expand the bubble.
This works for me, because I know that the osmotic pressure of the 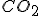 is going to depend on how much was dissolved in the water to begin with. My conclusion, roughly speaking: drinks with bigger bubbles had more carbon-dioxide dissolved in them to start with than drinks with smaller bubbles. At least, that’s my working hypothesis for now, disregarding lots of other possible effects in bubbles. I’ll have to do some experiments to see whether it holds up.
is going to depend on how much was dissolved in the water to begin with. My conclusion, roughly speaking: drinks with bigger bubbles had more carbon-dioxide dissolved in them to start with than drinks with smaller bubbles. At least, that’s my working hypothesis for now, disregarding lots of other possible effects in bubbles. I’ll have to do some experiments to see whether it holds up.
This is just my answer for the moment, my provisional and incomplete understanding. It’s not a subject you can just look up on Wikipedia and be done with. (The articles at about.com that discussed bubbles in sodas I didn’t find credible.) I found several references (one, two, three) that, in journalistic fashion, touted the research of University of Reims’ Gerard Liger-Belair as “Unlocking the Secrets of Champagne Bubbles”, but in fact it was a contribution to nucleation and had nothing to offer about bubble size. The third reference, by the way, has a glaring error in the second sentence, and the rest of the text suggests that the author of the story had little understanding of what was being talked about.
Here, in fact, is a piece about bubbles by Liger-Belair (mentioned in the last paragraph), called “Effervescence in a glass of champagne: A bubble story“. It’s a nice read but it skirts ever so gracefully past the question of bubble size.
As we say in the biz: more research is indicated.
———-
* My usual contention being that most of the work of finding the answer lies in asking a good question.
# What might “immediate vicinity” mean, you ask? In physicist fashion, I’m going to suggest that length-scales in the problem will be roughly determined by the size of the bubbles, so let’s take “immediate vicinity” to mean anything within 1, or 2, or maybe 3 bubble radii. (On closer examination we’d have to consider thermal diffusivity and mass-species diffusivity and such things, but that’s for a more sophisticated analysis.)
%“San Benedetto” is the brand of effervescent water that we prefer here at Björnslottet, in case you were wondering.
**But why! Bubbles first start (“nucleate”) either around small impurities or bits of dust in the fluid, or just from fluctuations in the local concentration of bubble stuff. Let’s leave that as an interesting question for another time and just assume they get started somehow.
Oct
17
Posted by jns on
October 17, 2007
Here is “Science @ NASA” again, sending me another interesting story with pretty pictures. This one — they say for shock value — is about “undular bores”. What they’re talking about is waves in the atmosphere that show up dramatically in cloud patterns.
I have a personal interest in all things waves because they were one of the things I studied in my former life as a physicist. They were waves in many forms that interested me, too, since I studied fluid motions, in which one can find physical waves, and field phenomenon, in which the waves are mathematically abstract but still represent real phenomenon.
In looking at these wave pictures coming up, it might be fun to know that in the ocean — or on any water surface — waves come in two types, call them “waves” (the big ones) and “ripples” (the little ones). Ripples are about finger sized, while waves are more body sized. Both are caused by disturbances, generally wind, but they undulate for different reasons. Ripples ripple because of the surface tension of the water; waves wave because of gravity, or buoyancy, in the water. Most water waves in the ocean, and those that break on shorelines, are generated by strong winds associated with storms that can be thousands of miles away.
Anyway, air also has buoyancy (remember: hot air rises, cool air sinks — the hot air is buoyant relative to the cool) and can sometimes show some very large scale waves, with wavelengths of about a mile. When there are clouds around they can make the waves dramatically visible. They can be caused by storms moving about as high-pressure centers collide with low-pressure centers and hot-air masses encounter cool-air masses.
Here’s Tim Coleman of the National Space Science and Technology Center (NSSTC) in Huntsville, Alabama:
“These waves were created by a cluster of thunderstorms approaching Des Moines from the west,” he explains. “At the time, a layer of cold, stable air was sitting on top of Des Moines. The approaching storms disturbed this air, creating a ripple akin to what we see when we toss a stone into a pond.”
Undular bores are a type of “gravity wave”—so called because gravity acts as the restoring force essential to wave motion. Analogy: “We’re all familiar with gravity waves caused by boats in water,” points out Coleman. “When a boat goes tearing across a lake, water in front of the boat is pushed upward. Gravity pulls the water back down again and this sets up a wave.”
[excerpt from "Giant Atmospheric Waves Over Iowa", Science @ NASA for 11 October 2007.]
There are two gorgeous visuals to see by clicking the link. The first is a video of the undular bores over Iowa. I’d suggest watching the animated gifs rather than the video because the gifs extract just the interesting parts between 9:25 and 9:45, and it keeps playing.
Then, just below that, don’t miss the radar photograph, which shows the train of waves with stunning clarity.
Now, as if that weren’t enough, I found this cool video on YouTube, intended to demonstrate “Gravity Waves” in the atmosphere, of which it is a beautiful example. But wait! Incredibly, this video also shows undular bores, over Iowa (but Tama, rather than Des Moines), as recorded by the same television station, KCCI!
Sep
23
Posted by jns on
September 23, 2007
I can’t help myself now. I’ve just read through another paper by some of the  -algorithm people*, and they provide two fascinating equations from the history of computing
-algorithm people*, and they provide two fascinating equations from the history of computing  . Although they have been used in practice, my purpose here is just to look at them in amazement.
. Although they have been used in practice, my purpose here is just to look at them in amazement.
This first one is an odd and ungainly expression discovered by the Indian mathematical genius Ramanujan (1887–1920):#
![\Large\frac{1}{\pi} \quad = \quad \frac{\sqrt{8}}{9801}\ \sum_{n=0}^{\infty} \ \frac{(4n)!}{(n!)^4}\ \frac{[1103\ +\ 26390n]}{396^{4n}} \Large\frac{1}{\pi} \quad = \quad \frac{\sqrt{8}}{9801}\ \sum_{n=0}^{\infty} \ \frac{(4n)!}{(n!)^4}\ \frac{[1103\ +\ 26390n]}{396^{4n}}](http://scienticity.net/sos/latexrender/pictures/0e19bab91ae3a23a4178e173356bab7f.gif)
One extraordinary fact about this series is that it converges extremely rapidly: each additional term adds roughly 8 digits to the decimal expansion.
The second has been developed much more recently by David and Gregory Chudnovsky (universally called “The Chudnovsky Brothers”) and used in their various calculations of  . In 1994 they passed the four-billionth digit.& This is their “favorite identity”:
. In 1994 they passed the four-billionth digit.& This is their “favorite identity”:
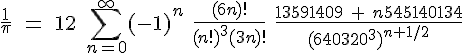
———-
* D.H. Bailey, J.M. Borwein, and P.B. Borwein, “Ramanujan, Modular Equations, and Approximations to Pi or How to Compute One Billion Digits of Pi”, American Mathematical Monthly, vol. 96, no. 3 (March 1989), pp. 201–219; reprint available online.
# One purpose of the paper was to show how this formula is related — deviously, it turns out, although a mathematician would say “straightforward” after seeing the answer — to things called elliptic functions.
&Okay, it was 18 May 1994 and the number of digits they calculated was 4,044,000,000. They used a supercomputer that was “largely home-built”. This record number of digits did not remain a record for long, however.
Sep
22
Posted by jns on
September 22, 2007
How innocently it all begins, sometimes. For some reason a day or two ago I decided I would take a few google-moments and look into modern computational formulæ that are use to calculate the value of  . What a loaded question that turned out to be! Before I’d reached a point to pause and write — and I’m not confident that I’m there yet — I’ve read several mathematics papers, installed software so that I could type equations in the blog [1], thought more about number theory and complex analysis than I have for years, and even gave Isaac a short lecture on infinite series with illustrative equations written on the Taco Bell tray liner. Poor Isaac.
. What a loaded question that turned out to be! Before I’d reached a point to pause and write — and I’m not confident that I’m there yet — I’ve read several mathematics papers, installed software so that I could type equations in the blog [1], thought more about number theory and complex analysis than I have for years, and even gave Isaac a short lecture on infinite series with illustrative equations written on the Taco Bell tray liner. Poor Isaac.
Suppose you want to calculate the value of  . The number
. The number  , you may recall, is transcendental and therefore irrational — serious categories of numbers whose details don’t matter much except to remember that
, you may recall, is transcendental and therefore irrational — serious categories of numbers whose details don’t matter much except to remember that  , written as a decimal number, has digits after the decimal point that never repeat and never end. Most famously
, written as a decimal number, has digits after the decimal point that never repeat and never end. Most famously  relates the diameter of a circle,
relates the diameter of a circle, 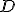 , to its radius,
, to its radius, 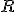 , in this manner:
, in this manner:
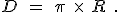
There are also a surprising number of other mathematical equations involving  that have no obvious relationship with circles. One very important and useful type of relationship involves infinite series. Infinite series are written in a very compact mathematical notation that will look very inscrutable if it’s unfamiliar, but don’t be alarmed, please, because the idea is relatively simple. Here’s an example:
that have no obvious relationship with circles. One very important and useful type of relationship involves infinite series. Infinite series are written in a very compact mathematical notation that will look very inscrutable if it’s unfamiliar, but don’t be alarmed, please, because the idea is relatively simple. Here’s an example:
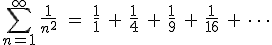
The big greek letter, capital sigma (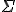 ), is the symbol that signals the series operation. The letter
), is the symbol that signals the series operation. The letter 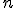 underneath the sigma is the index. The index is set in sequence to a series of integer values, in this case starting at one (because
underneath the sigma is the index. The index is set in sequence to a series of integer values, in this case starting at one (because 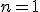 ), and ending with infinity, as specified by the number on top. Then, for each value of
), and ending with infinity, as specified by the number on top. Then, for each value of 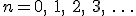 , the letter
, the letter 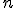 is replaced with that number in the mathematical expression following the big sigma and the successive terms are added together, the operation suggested by the sequence of fractions following the equals sign. (Feel free to look at the equation and think about it and look and think, if it’s new to you. Mathematics is rarely meant to be read quickly; it takes time to absorb.)
is replaced with that number in the mathematical expression following the big sigma and the successive terms are added together, the operation suggested by the sequence of fractions following the equals sign. (Feel free to look at the equation and think about it and look and think, if it’s new to you. Mathematics is rarely meant to be read quickly; it takes time to absorb.)
The other important idea about the series that we have to look at is the idea of convergence, a property of the series meaning that as one adds on each new term the result (called the partial sum, for obvious reasons) gets closer and closer to some numerical value (without going over!). It is said to converge on that value, and that value is known as the limit of the successive partial sums. [2]
Provided that the series converges, the limit of the partial sums is usually treated simply as the value of the series, as thought one could indeed add up the infinite number of terms and get that value.
It turns out that the series we wrote above (the solution to the so-called “Basel problem”) does indeed have a value (i.e., the partial sums converge to a limit) — a rather remarkable value, actually, given our interest in 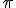 :
:
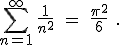
Really, it does. [3]
This equation also gives us a good hint of how the value of  is calculated, in practical terms, and this has been true since at least the time of Newton, whether one is calculating by hand or by digital computer. One finds a convenient expression that involves an infinite series on one side of the equals sign and
is calculated, in practical terms, and this has been true since at least the time of Newton, whether one is calculating by hand or by digital computer. One finds a convenient expression that involves an infinite series on one side of the equals sign and  on the other side and starts calculating partial sums. The trick is to find a particularly clever series that converges quickly, so that each new term added to the partial sum gets you closer to the limit value as fast as possible.
on the other side and starts calculating partial sums. The trick is to find a particularly clever series that converges quickly, so that each new term added to the partial sum gets you closer to the limit value as fast as possible.
It should come as no surprise that there are an infinite number of equations involving  with reasonable convergence properties that could be used to calculate its value, and an astounding number that have actually been used to do that. [4]
with reasonable convergence properties that could be used to calculate its value, and an astounding number that have actually been used to do that. [4]
It may also be no great surprise to hear that new equations are discovered all the time, although a new type of equation is rather more rare. Now, this part is a bit like one of those obscure jokes where we have to have some background and think about it before we get it. [5]
This is where my innocent investigation into calculating  took an unexpected turn. Let me quote the fun introduction to a paper by Adamchik and Wagon [6] :
took an unexpected turn. Let me quote the fun introduction to a paper by Adamchik and Wagon [6] :
One of the charms of mathematics is that it is possible to make elementary discoveries about objects that have been studied for millenia. A most striking example occurred recently when David Bailey of NASA/Ames and Peter Borwein and Simon Plouffe of the Centre for Experimental and Computational Mathematics at Simon Fraser University (henceforth, BBP) discovered a remarkable, and remarkably simple new formula for  . Here is their formula:
. Here is their formula:
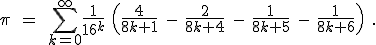
The original paper in which Bailey, Borwein, and Plouffe published this result appeared in 1997. [7]
Don’t freak out, just breathe deeply and look at it for a bit. [8] How they came by this equation is an interesting story in itself, but not one to go into here. It’s enough to know that it can be proven to be correct. (In fact, Adamchik and Wagon actually say “The formula is not too hard to prove…”; if you didn’t read note #5, now would be a good time!)
Isn’t it remarkable looking! I saw it and my reaction was along the lines of “how could  ever be equal to that thing?” This thing, by the way, is referred to as the “BBP formula” or the “BBP algorithm”. And then the talk about this equation started to get a little weird and my original train of through about how to calculate
ever be equal to that thing?” This thing, by the way, is referred to as the “BBP formula” or the “BBP algorithm”. And then the talk about this equation started to get a little weird and my original train of through about how to calculate  derailed.
derailed.
People wrote about the BBP algorithm in very admiring terms, like “the formula of the century”, which started to sound like hyperbole, but really wasn’t. Then I tripped over some statements like this one [9] :
Amazingly, this formula is a digit-extraction algorithm for  in base 16.
in base 16.
Now, there’s a statement I had to pause and think for awhile to make some sense out of.
The “base 16″ part was easy enough. Usually we see the decimal expansion of  written in our everyday base 10 (this is truncated, not rounded):
written in our everyday base 10 (this is truncated, not rounded):
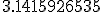
In base 16 the expansion looks like this (also truncated) [10] :
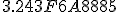
In the same way that the digits after the decimal point in the base-10 expansion means this:
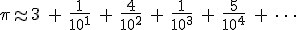
the hexadecimal expansion means simply this:
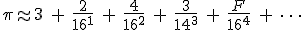
where the hexadecimal digits “A, B, C, D, E, and F” have the decimal values “10, 11, 12, 13, 14, and 15″.
For quite awhile I didn’t get the notion that it was a “decimal extraction algorithm”, which I also read to mean that this algorithm could be used to compute the 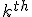 digit in the hexadecimal representation without calculating all the preceding digits.
digit in the hexadecimal representation without calculating all the preceding digits.
Now, that’s an amazing assertion that required understanding. How could that be possible. You’ve seen enough about series formulæ for  to see that the way one calculates is to keep grinding out digits until you get to, say, the millionth one, or the billionth one, which can take a long time.
to see that the way one calculates is to keep grinding out digits until you get to, say, the millionth one, or the billionth one, which can take a long time.
If only I had written down first thing the equation I wrote down above for how the various hexadecimal digits add together as the numerators of powers of (1/16), it would have been obvious. Look back now at the BBP equation. See that factor
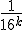
that comes right after the big sigma? That’s the giant clue about the “digit-extraction” property. If the expression in the parentheses happened to be a whole number between decimal values 0 and 15, then the 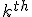 term would be exactly the
term would be exactly the 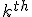 digit in the hexadecimal expansion of
digit in the hexadecimal expansion of  .
.
That’s an amazing idea. Now, it’s not exactly the 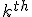 digit, because that expression doesn’t evaluate to a whole number between 0 and F (hexadecimal). Instead, it evaluates to some number smaller than 1, but not incredibly smaller than one. (If, e.g., k = 100 it’s about 0.000002).
digit, because that expression doesn’t evaluate to a whole number between 0 and F (hexadecimal). Instead, it evaluates to some number smaller than 1, but not incredibly smaller than one. (If, e.g., k = 100 it’s about 0.000002).
Philosophically, and mathematically, it’s important that it’s not exactly a digit-extraction algorithm, but an approximate one. You can’t just calculate the millionth digit just by setting k = 1,000,000 and computing one term.
Remarkably enough, though, the BBP algorithm can be, in effect, rearranged to give a rapidly converging series for the millionth digit, if you choose to calculate that particular digit. [11]
Now, in the realm of true hyperbole, I read some headlines about the BBP algorithm that claimed the algorithm suggested that there was some pattern to the digits of  and that the digits are not truly random — words evidently meant to be spoken in a hushed voice implying that the mysteries of the universe might be even more mysterious. Bugga bugga!
and that the digits are not truly random — words evidently meant to be spoken in a hushed voice implying that the mysteries of the universe might be even more mysterious. Bugga bugga!
Now, that business about how maybe now the digits of  aren’t random after all — it’s hogwash because the digits of
aren’t random after all — it’s hogwash because the digits of  never were random to begin with. It’s all a confusion (or intentional obfuscation) over what “random” means. The number
never were random to begin with. It’s all a confusion (or intentional obfuscation) over what “random” means. The number  is and always has been irrational, transcendental, unchangeably constant, and the individual digits in the decimal (or hexadecimal) expansion are and always have been unpredictable, but not random.
is and always has been irrational, transcendental, unchangeably constant, and the individual digits in the decimal (or hexadecimal) expansion are and always have been unpredictable, but not random.
They cannot be random since  has a constant value that is fixed, in effect, by all the mathematical expressions that it appears in. The millionth digit has to be whatever it is in order to make
has a constant value that is fixed, in effect, by all the mathematical expressions that it appears in. The millionth digit has to be whatever it is in order to make  satisfy the constraints of the rest of mathematics. It’s the case that all of the digits are essentially fixed, and have been forever, but we don’t know what their values are until we compute them.
satisfy the constraints of the rest of mathematics. It’s the case that all of the digits are essentially fixed, and have been forever, but we don’t know what their values are until we compute them.
Previously, to know the millionth digit we had to calculate digits 1 through 999,999; with the BBP algorithm that’s not necessary and a shorter calculation will suffice, but that calculation still involves a (rapidly converging) infinite series. Individual digits are not specified, not really “extracted”, but they are now individually calculable to arbitrary precision. And, since individual digits are whole numbers with decimal values between 0 and 15, reasonable precision on calculating the digit tells you what the actual digit is.
Still, it is an amazing formula, both practically and mathematically. And now I just tripped over a paper by the BBP authors about the history of calculating  . [12] Maybe I can finally get my train of thought back on track.
. [12] Maybe I can finally get my train of thought back on track.
———-
[1] At the core is mimeTeX, a remarkable piece of software written by John Forkosh that makes it possible for those of us familiar with TeX, the mathematical typesetting language created some two decades ago by mathematician Donald Knuth, to whip up some complicated equations with relative ease.
[2] This limit is the same concept that is central in calculus and has been examined in great care by anyone who has taken a calculus course, and even more intensively by anyone who’s taken courses in analysis. But, for the present, there’s no need to obsess over the refinements of the idea of limits; the casual idea that comes to mind in this context is good enough.
[3] It was proven by Leonhard Euler in 1735. If you really, really want to see a proof of this assertion, the Wikipedia article on the Basel problem will provide enough details to satisfy, I expect.
[4] The page called “Pi Formulas” at Wolfram MathWorld has a dazzling collection of such equations.
[5] There is an old joke of this type about mathematicians. We used to say “The job of a mathematician is to make things obvious.” This refers to the habit among those professionals of saying “obviously” about the most obscure statements and theorems. Another version of the joke has a mathematician writing lines of equations on a chalkboard during class and reaching a point when he says “it’s obvious that…”, at which point he pauses and leaves the room. The class is mystified, but he returns in 20 minutes, takes up where he left off in his proof, saying “Yes, it is obvious that….”
The version of this that one finds in math and physics textbooks is the phrase, printed after some particularly obscure statement, “as the reader can easily show.” That phrase appeared once in my graduate text on electrodynamic (by J.D. Jackson, of course, for those in the know), and showing it “easily” took two full periods of my course in complex analysis.
[6] Victor Adamchik and Stan Wagon, “ : A 2000-Year Search Changes Direction“, Mathematica in Education and Research, vol. 5, no.1, (1996), pp, 11–19.
: A 2000-Year Search Changes Direction“, Mathematica in Education and Research, vol. 5, no.1, (1996), pp, 11–19.
[7] David Bailey, Peter Borwein, and Simon Plouffe, “On the Rapid Computation of Various Polylogarithmic Constants”, Mathematics of Computation, vol. 66, no. 218 (April 1997), pp. 903–913; reprint available online.
[8] And remember that writing the 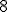 next to the
next to the 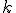 just means to multiply them together. Although I used
just means to multiply them together. Although I used 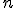 as the index in the example above, here the index is called
as the index in the example above, here the index is called 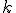 — the name doesn’t matter, which is why it’s sometimes called a dummy index.
— the name doesn’t matter, which is why it’s sometimes called a dummy index.
[9] For an example: Eric W. Weisstein, “BBP Formula“, MathWorld–A Wolfram Web Resource, accessed 23 September 2007 [the autumnal equinox].
[10] “Sample digits for hexa-decimal digits of pi“, 18 January 2003.
[11] If you want to know the details, there’s a nice paper written by one of the original authors a decade later in which he shows just how to do it: David H. Bailey, “The BBP Algorithm for Pi“, 17 September 2006, (apparently unpublished).
[12] David H. Bailey, Jonathan M. Borwein, Peter B. Borwein, and Simon Plouffe, “The Quest for Pi”, Mathematical Intelligencer, vol. 19, no. 1 (Jan. 1997), pp. 50–57; reprint available online.
May
27
Posted by jns on
May 27, 2007
Via NASA’s Earth Observatory mailing list my attention was drawn to their newly freshened Global Warming fact sheet, written by Holli Riebeek (dated 11 May 2007), and I wanted to take this space to draw more attention to it.
As most of my readers will know, there’s a great deal of misleading disinformation and obfuscation in our current global-warming “debate” here in the US, a concerted effort by some business and political forces to confuse the public into thinking that there is no scientific consensus on anthropogenic climate change, i.e., global warming because of carbon-dioxide (and other greenhouse gas) emissions being pumped into the atmosphere from human sources.
There is consensus among scientists working in the field; how and why and what it all means is nicely summarized in this short, succinct, and accurate fact sheet. Without being patronizing and without distorting the information, it’s a clear and understandable presentation of what we (the science “we”) know about global warming, the trends, the causes, and the likely or possible consequences.
In particular, the author addresses this question:
But why should we worry about a seemingly small increase in temperature? It turns out that the global average temperature is quite stable over long periods of time, and small changes in that temperature correspond to enormous changes in the environment.
It keeps popping up as a joke, especially during wintertime or a cool day in the summer, when people casually say “I wouldn’t mind a bit if it were a degree or two warmer”.
What is missing in this superficial understanding is a realization that, overall, the Earth’s temperatures are quite stable on average, and that very small changes in average temperatures can have very, very large effects on weather patterns and that those changes in weather patters lead to subsequently surprisingly large shifts in the weather we get at any particular location. In other contexts this is sometimes called “the butterfly effect”: consequences can be out of all proportion (i.e., nonlinear) to the causes. Ice ages have been accompanied by changes in the average global temperature of only about 5°C — which doesn’t sound all that big.
This is discussed quite well in the fact sheet, and summarized (in part) this way:
Potential Effects
The most obvious impact of global warming will be changes in both average and extreme temperature and precipitation, but warming will also enhance coastal erosion, lengthen the growing season, melt ice caps and glaciers, and alter the range of some infectious diseases, among other things.
For most places, global warming will result in more hot days and fewer cool days, with the greatest warming happening over land. Longer, more intense heat waves will become more frequent. High latitudes and generally wet places will tend to receive more rainfall, while tropical regions and generally dry places will probably receive less rain. Increases in rainfall will come in the form of bigger, wetter storms, rather than in the form of more rainy days. In between those larger storms will be longer periods of light or no rain, so the frequency of drought will increase. Hurricanes will likely increase in intensity due to warmer ocean surface temperatures.
It’s a good piece and a few minutes invested in reading through it will arm the reader with better understanding that will help cut a confident path through the thicket of opinions and misinformation that have clogged the information superhighway on the issue lately.
May
11
Posted by jns on
May 11, 2007
Here’s a quick question with a pedagogical purpose. Would you buy a battery from this man?
“The energy capacity of batteries is increasing 5 percent to 8 percent annually, but demand is increasing exponentially,” Mr. Cooper[, vice president for business development of PolyFuel Inc., a company working on battery technology,] said.
[Damon Darlin and Barnaby J. Feder, "Need for Battery Power Runs Into Basic Hurdles of Science", New York Times, 16 August 2006.]
Forget basic hurdles of science, the basic hurdle here would seem to be an executive in a technical industry who doesn’t understand what exponential growth is.
In short: growth of something that is proportional to the current size of that thing is exponential growth. Thus, demand for batteries that grows 5% to 8% annually — i.e., 0.05 to 0.08 times current demand — is exponential growth.
The constant that governs how fast something grows exponentially is the “growth rate”. Small growth rate = slow growth; large growth rate = fast growth. In symbols, an exponential function of time, t, is
f(t) = A × est
where A is a constant amplitude and s is the growth rate. If s is relatively large, f(t) changes values rapidly; is s is very small, f(t) changes values slowly. If s happens to be a negative number, f(t) disappears over time, quickly or slowly depending on the size of s. The letter ‘e’ represents the base of natural logarithms. Why it shows up in the exponential function takes some explanation; for now, just think of it as a constant number nearly equal to 2.17 and don’t lose any sleep over it.*
Many people think “exponential growth” means “grows really, really quickly”, but this is a misconception. It is true that power-law growth is generally faster than algebraic growth (for instance, multiplying a number over and over again by some number, say, 47) all other things being equal, but any particular exponential function will grow slowly or quickly depending on its growth rate. Think of a $0.15 deposit in a bank account that pays compound interest; the account grows exponentially but it’s going to be awhile before you’re a millionaire.
So please, please can we stop saying things like “Wow! That growth is so exponential! It’s huge!”
And if I were you, I don’t think I’d buy a battery from Mr. Cooper, either.
———-
* In fact, ‘e’ is irrational (not expressible as the fraction of two integers, or whole numbers) and transcendental (not the solution to an algebraic equation, which is to say a polynomial with rational coefficients and integer powers). But that’s a lot of other story that we needn’t go into right now.
Mar
20
Posted by jns on
March 20, 2007
Speaking of the Vernal Equinox, many people were — speaking of it — yesterday but occasionally with some imprecision, saying that spring “officially” arrived at about 2007 EDT. They would be better off saying “astronomically” arrived, since there’s nothing “official” about it: no international committee meets to set the time of the arrival of springtime. Instead, we have chosen to relate the change of seasons to clearly and precisely defined events related to the apparent motion of the sun, events that have been noted since antiquity.
Because of the tilt of the Earth’s axis of rotation (about 23.5°) relative to the plane of its orbit around the Sun, the zenith of the Sun (i.e., it’s largest angle above the horizon each day) changes with the seasons; it’s higher in the sky during summer and lower during winter.* In other words, the Sun appears to move not only along a path across the sky (the “ecliptic”), but that path appears to move higher and lower as the year progresses.
Now, imagine a line from the center of the Earth to the Sun; where the line passes through the surface of the Earth is the point at which the Sun, at that moment, can be said to be directly overhead. Let’s call this line the “Sun Chord” — so far as I know it has no generally recognized name, and this name sounds harmonious.
As the days of the year pass, the apparent motion of the sun in the sky — or the intersection of the Sun Chord with the Earth’s surface — traces out a squished figure-eight (the “analemma“);# the exact shape of the analemma depends on the location of the observer.
As the Sun executes its stately analemmic dance, there are fixed extremes to its motion. When the Sun appears at its northern-most point, the Sun Chord passes through the “Tropic of Cancer”, which is at a latitude of about 23.5°N; similarly, when the Sun appears at its Southern-most point, the Sun Chord passes through the “Tropic of Capricorn”, is at a latitude of about 23.5°S. It is not a coincidence that these latitudes have the same angles as the tilt of the Earth’s axis; it is a consequence of geometry. The Sun’s passing through these extreme points is called a “solstice”. In the northern hemisphere we often call the solstice that occurs in June the “summer solstice”, and the solstice in December the “winter solstice”.
Also during the year there are two times — very nearly 6 months apart and 3 months separated from each solstice — when the Sun Chord passes through the Earth’s equator, i.e., when the sun is directly overhead at the equator. When the Sun appears to be moving in a northerly direction this point is the “vernal equinox” (or “spring equinox”); when the Sun is moving in a southerly direction this point is the “autumnal equinox”. “Equinox”, of course, means “equal night”, a name given because the amount of daylight and nighttime are [roughly] equal everywhere on the Earth (except extremely near the poles, which are singular points in this geometrical picture).
And now to the point of this essay. Equinox and solstice times are mathematical concepts describing astronomical events. They occur at well-defined times that can be determined with as much precision as one would care to take. We can calculate to any number of decimal places the exact moment when the Sun Chord intersects the equator, making it possible to say that the vernal equinox occurred at seven minutes past eight (EDT) last evening.
Now, whether spring “officially” started then is another matter entirely, a matter of convention and history, but not a geometric necessity.
[After I'd started writing this piece, Isaac sent me a link to an essay on the vernal equinox in the New York Times by Natalie Angier, "The Tilted Earth at Its ‘Equal Night of Spring’ ", which adds some cultural considerations to the topic. The illustration is kind of cute, too, although it does suggest something more along the lines of a "martini equinox".]
———-
*This statement is true in both northern and southern hemispheres, but the seasons are reversed, which should become clear with a moment’s reflection.
#Yes, this is true at the equator as well: the apparent motion of the sun describes an analemma. It is a common misconception that the sun at the equator is always overhead; what is true is that day and night at the equator are always equal, but there is apparent motion of the sun by about 23.5° to both sides of vertical.
Dec
07
Posted by jns on
December 7, 2006
This is the day of the year, 7 December, when I celebrate my own festival of light to welcome the return of the sun.
No, it is not the shortest day of the year, the day with the least amount of sunlight where I am (about 39 degrees north, 76 degrees, 46 minutes west — but the effect only depends on latitude), because it is not the Winter Solstice, which occurs about 21 December.
It is, however, the earliest sunset of the year, a more interesting inflection point. Since I rarely experience sunrise, at least by choice, this is psychologically much more important. Beyond today, the day will appear to me ever so slowly to be getting longer again because after today the sun will start going down later in the evening.
The effect is hardly noticeable at first,* but by the time we get to the Solstice the day-to-day change in sun-setting time will be noticeably larger. I was happy when I learned about this, the pre-Solstice early-sun-setting day, because it explained for me the feeling I’d always had that once we got past the Solstice it seemed as though the days started getting longer very quickly.#
The reason for the phenomenon is tougher to explain than to comprehend; I looked at three different versions (one, two, and three), none of which struck me as entirely satisfactory, but feel free to have a go. To make a long story short, I can point out that if the earth weren’t tilted then this curious misalignment of times wouldn’t happen. But then, neither would the seasons, and neither would the apparent position of the sun’s zenith in the sky** change from day to day.##
Regardless of all that, I’m always happy to see the sun starting to linger longer at the end of each day.
———-
*For those with a calculus vocabulary, the curve of earliest sunset times as a function of date has just passed an extremum and the derivative is still very near zero.
#Finally, this gives you something to do with those previously useless reports in the newspaper or in the nightly weather forecast that give you sunset and sunrise time: plot the curves for yourself and see when the minima and maxima in sunset and sunrise occur at your latitude.
**Known as the “analemma”, the figure-8 shape found on precision sun-dials and on globes of the Earth.
##How much it changes day-to-day depends on one’s latitude and is described by the grandly named “Equation of Time”.
Apr
07
Posted by jns on
April 7, 2006
I have a friend upon whom I can rely to send me, with some regularity, unbelievable photos and incredible stories, most of which turn out in the end to be fabricated photos and urban legends. Someplace in the forwarding of these things, someone will often add a wishy-washy “I don’t know if this is true, but….” and then carry on anyway.
Sure enough, the last photo I got from him was a beauty: an arctic landscape with a bright, tiny sun hovering on the horizon and, above it, an enormous crescent moon. It was quite a lovely image. The text with it said
This is the sunset at the North Pole with the moon at its closest point. And, you also see the sun below the moon. An amazing photo and not one easily duplicated. You may want to save this and pass on to others.
“…not easily duplicated” is correct! While the image is pretty, it’s a complete fabrication, and I’d like to think that should have been obvious to anyone seeing it. But then, I’d like to think a lot of things that turn out to have nothing to do with reality.
Happily, snopes.com says plainly that the photograph is a fabrication, created digitally by a German astrophysics student. (Follow the link for the details and to see the image.)
However, Snopes missed their chance to state the obvious: the photograph could not possibly be a real image of “sunset at the North Pole” for one simple reason that everyone should be able to spot — the image of the moon, compared to the image of the sun, is far, far too large.
But how could anyone be expected to know this*, you ask? Well, I claim, nearly everyone knows the cause of total solar eclipses, even if they’ve never seen one: the moon passes between the Earth and the sun and exactly covers the disk of the sun for a short time.
The simple deduction, then, is that the apparent size of the moon, as seen from the Earth, is very nearly the same as the apparent size of the sun. Thus we know that this image, in which the moon is some 20 times the size of the sun, must be a fabrication.
———-
* This is an interesting question, particularly since in films, night scenes are often created with a looming, full moon shot with a telephoto lens; the same is rarely done for the sun, unless it is near the horizon into which the movie’s heroes are riding. People often seem ready to accept that the apparent size of the moon is substantially larger than it is in reality, whereas they seem to imagine the apparent size of the sun to be rather smaller than it actually is. These mistaken notions are exploited in the north-pole “sunset” image.
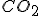 ) in effervescent water, say “San Benedetto” brand.% Now, bubbles have very few features of any physical importance: their sizeis an important one, and the interface between the inside and outside of the bubble, which we might call the surface of the bubble. Some chemical properties of the stuff inside and outside the bubble might matter, too, but let’s save that for a moment.
) in effervescent water, say “San Benedetto” brand.% Now, bubbles have very few features of any physical importance: their sizeis an important one, and the interface between the inside and outside of the bubble, which we might call the surface of the bubble. Some chemical properties of the stuff inside and outside the bubble might matter, too, but let’s save that for a moment. -algorithm people*, and they provide two fascinating equations from the history of computing
-algorithm people*, and they provide two fascinating equations from the history of computing ![\Large\frac{1}{\pi} \quad = \quad \frac{\sqrt{8}}{9801}\ \sum_{n=0}^{\infty} \ \frac{(4n)!}{(n!)^4}\ \frac{[1103\ +\ 26390n]}{396^{4n}} \Large\frac{1}{\pi} \quad = \quad \frac{\sqrt{8}}{9801}\ \sum_{n=0}^{\infty} \ \frac{(4n)!}{(n!)^4}\ \frac{[1103\ +\ 26390n]}{396^{4n}}](http://scienticity.net/sos/latexrender/pictures/0e19bab91ae3a23a4178e173356bab7f.gif)
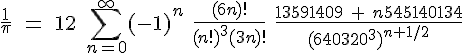
 , to its radius,
, to its radius, 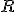 , in this manner:
, in this manner: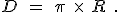
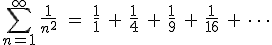
 ), is the symbol that signals the series operation. The letter
), is the symbol that signals the series operation. The letter 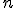 underneath the sigma is the index. The index is set in sequence to a series of integer values, in this case starting at one (because
underneath the sigma is the index. The index is set in sequence to a series of integer values, in this case starting at one (because 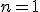 ), and ending with infinity, as specified by the number on top. Then, for each value of
), and ending with infinity, as specified by the number on top. Then, for each value of 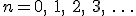 , the letter
, the letter 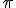 :
: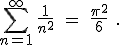
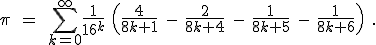
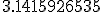
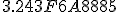
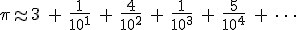
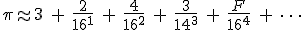
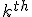 digit in the hexadecimal representation without calculating all the preceding digits.
digit in the hexadecimal representation without calculating all the preceding digits. 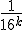
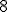 next to the
next to the 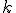 just means to multiply them together. Although I used
just means to multiply them together. Although I used