23
Two More Bites of Pi
Posted by jns on 23 September 2007I can’t help myself now. I’ve just read through another paper by some of the 
-algorithm people*, and they provide two fascinating equations from the history of computing . Although they have been used in practice, my purpose here is just to look at them in amazement.
This first one is an odd and ungainly expression discovered by the Indian mathematical genius Ramanujan (1887–1920):#
![\Large\frac{1}{\pi} \quad = \quad \frac{\sqrt{8}}{9801}\ \sum_{n=0}^{\infty} \ \frac{(4n)!}{(n!)^4}\ \frac{[1103\ +\ 26390n]}{396^{4n}}](http://scienticity.net/sos/latexrender/pictures/0e19bab91ae3a23a4178e173356bab7f.gif "\Large\frac{1}{\pi} \quad = \quad \frac{\sqrt{8}}{9801}\ \sum_{n=0}^{\infty} \ \frac{(4n)!}{(n!)^4}\ \frac{[1103\ +\ 26390n]}{396^{4n}}")
One extraordinary fact about this series is that it converges extremely rapidly: each additional term adds roughly 8 digits to the decimal expansion.
The second has been developed much more recently by David and Gregory Chudnovsky (universally called “The Chudnovsky Brothers”) and used in their various calculations of . In 1994 they passed the four-billionth digit.& This is their “favorite identity”:
———-
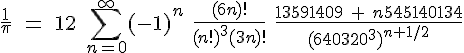
* D.H. Bailey, J.M. Borwein, and P.B. Borwein, “Ramanujan, Modular Equations, and Approximations to Pi or How to Compute One Billion Digits of Pi”, American Mathematical Monthly, vol. 96, no. 3 (March 1989), pp. 201–219; reprint available online.
# One purpose of the paper was to show how this formula is related — deviously, it turns out, although a mathematician would say “straightforward” after seeing the answer — to things called elliptic functions.
&Okay, it was 18 May 1994 and the number of digits they calculated was 4,044,000,000. They used a supercomputer that was “largely home-built”. This record number of digits did not remain a record for long, however.