May
02
Posted by jns on 2 May 2008
Just in case you came in late, or you don’t remember the events of the time, and never realized the terror that could be induced by toasters, Robert Park updates us on the utter lack of danger associated with electromagnetic fields (EMF).
HYBRIPHOBIA: REMEMBER WHEN POWER LINES CAUSED CANCER?
EMF stopped causing cancer in 1997, but no one bothered to tell Jim Motavalli, who wrote an Automobile column in the Sunday New York Times about the risks of EMF in hybrids. According to Motavalli the National Cancer Institute studied the cancer risks associated with electromagnetic fields. And so it did – but it couldn’t find any. You might think Motavalli would at least check the Archives of the New York Times. On July 3, 1997, the day the massive four-year NCI study of power lines and cancer appeared in the New England Journal of Medicine, Gina Kolata reported in the Times that the study was unambiguous and found no health effects associated with electromagnetic fields. An editorial in the same issue of the Journal put it in perspective: “Hundreds of millions of dollars have gone into studies that never had much promise of finding a way to prevent the tragedy of cancer in children. It is time to stop wasting our research resources.” It all began in 1979 when Nancy Wertheimer, an unemployed epidemiologist, and her friend Ed Leeper, drove around Denver looking for common environmental factors in the homes of childhood victims of leukemia. It practically jumped out at them – every home had electricity. Their study was so flawed it would have been laughed off but for Paul Brodeur, a scientifically-ignorant writer for The New Yorker. He wrote a series of terrifying articles about power lines and cancer that were collected in a 1989 book, Currents of Death.
[Robert Park, What's New, 2 May 2008.]
May
01
Posted by jns on 1 May 2008
The story, as it’s told online in National Geographic News,* goes like this.
n 1971, scientists transplanted five adult pairs of [Italian wall lizards] from their original island home in Pod Kopiste to the tiny neighboring island of Pod Mrcaru, both in the south Adriatic Sea[, off the coast of Croatia].
Genetic testing on the Pod Mrcaru lizards confirmed that the modern population of more than 5,000 Italian wall lizards are all descendants of the original ten lizards left behind in the 1970s.
However, the Pod Mrcaru/Italian wall lizards of today are no longer much like the original pair. It seems that the population has evolved some new digestive strategies–and parts!–along with a different head with a stronger jaw to go along with the new strategy. All this they managed to do in only 30 generations on the island.
As the report says, all of the current lizards have been tested genetically and are known to be descended from the original pair. It also turns out that the new lizards have displaced the aboriginal lizards on the island when the first pair were transplanted. There is no determination mentioned about whether the new lizard is a different species from the original pair.
Isn’t that interesting! Evolution in action, and on a surprisingly short time scale. How can this be possible though? Doesn’t evolution take ages and ages to accomplish change?
Yes and no. As our understanding of evolution (and natural selection) improves and deepens, it seems that evolution is anything but uniformly slow and uniformly steady.# Indeed, the more modern understanding is coming to terms with how genetic information is prepared, as it were, to make rapid changes when the occasion arises. Some of this is touched on in Sean Carroll’s book Endless Forms Most Beautiful.
Of course there is a political aspect to this report of scientific findings. Some evolution deniers will continue to deny that speciation is possible through evolution, but they will be seen to be wrong, probably sooner rather than later, too.
__________
*Kimberly Johnson, “Lizards Rapidly Evolve After Introduction to Island“, National Geographic News, 21 April 2008.
#Although I don’t really see the need to turn to the concept of Punctuated Equilibrium, as promoted by Eldredge & Gould to incorporate the nonuniformity. Doing so seems to me to caricature any realistic understanding of gradualism.
Apr
30
Posted by jns on 30 April 2008
 The image at right is a gorgeous rendering† of a mystifying object known as the Lorenz Attractor. It shares its name with Edward Lorenz, its discoverer, who died earlier this month at the age of 90.* Edward Lorenz is sometimes called “the father of chaos”, and the Lorenz attractor is the reason.
The image at right is a gorgeous rendering† of a mystifying object known as the Lorenz Attractor. It shares its name with Edward Lorenz, its discoverer, who died earlier this month at the age of 90.* Edward Lorenz is sometimes called “the father of chaos”, and the Lorenz attractor is the reason.
Lorenz was a mathematician and meteorologist. In the early 1960s he was using what is usually described as an “extremely primitive computer” (a “Royal McBee LPG-30″) to work out some numerical solutions to a relatively simple set of equations he was using to model atmospheric convection‡. They are a simple set of differential equations, not particularly scary, so we might as well see what they look like:
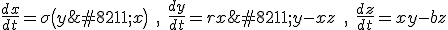
The 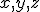 , by the way, are not spatial variables but instead more abstract variables that represent wind velocity, pressure, and temperature in the atmosphere. You can still think of them, though, as the three dimensions of an abstract “space” that is referred to as “phase space”.# The
, by the way, are not spatial variables but instead more abstract variables that represent wind velocity, pressure, and temperature in the atmosphere. You can still think of them, though, as the three dimensions of an abstract “space” that is referred to as “phase space”.# The 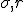 and
and 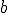 are parameters in the system, numbers that get set to some value and then left at that value; parameters allow the set of equations to describe a whole family of dynamical systems.
are parameters in the system, numbers that get set to some value and then left at that value; parameters allow the set of equations to describe a whole family of dynamical systems.
What happened next (in the dramatic flow of time) is a story that’s been told over and over. Here’s how the American Physical Society tells it:
He [Lorenz] kept a continuous simulation running on an extremely primitive computer [!], which would produce a day’s worth of virtual weather every minute. The system was quite successful at producing data that resembled naturally occurring weather patterns: nothing ever happened the same way twice, but there was clearly an underlying order.
One day in the winter of 1961, Lorenz wanted to examine one particular sequence at greater length, but he took a shortcut. Instead of starting the whole run over, he started midway through, typing the numbers straight from the earlier printout to give the machine its initial conditions. Then he walked down the hall for a cup of coffee, and when he returned an hour later, he found an unexpected result. Instead of exactly duplicating the earlier run, the new printout showed the virtual weather diverging so rapidly from the previous pattern that, within just a few virtual “months”, all resemblance between the two had disappeared.
At first Lorenz assumed that a vacuum tube had gone bad in his computer, a Royal McBee, which was extremely slow and crude by today’s standards. Much to his surprise, there had been no malfunction. The problem lay in the numbers he had typed. Six decimal places were stored in the computer’s memory: .506127. To save space on the printout, only three appeared: .506. Lorenz had entered the shorter, rounded-off numbers assuming that the difference [of] one part in a thousand was inconsequential.
["This Month in Physics History: 'Circa January 1961: Lorenz and the Butterfly Effect' ", APS News, January 2003.]
This was a shocking result. The system of equations he was studying was nonlinear, and it is well-known that nonlinear systems can amplify small differences — Lorenz did not discover nonlinear amplification as some have written. But this divergence of the solutions was extreme: after not much time the two solutions not only weren’t close, they were so far apart that it looked like they never had anything to do with each other. This is a characteristic known as extreme sensitivity to initial conditions.
What’s more, one could put in virtually identical initial conditions all day long and keep getting different results a little ways down the road. In fact, the state of the system at these later times was unpredictable in practical terms — the system was chaotic in behavior.
That chaotic behavior was shocking result number two. Chaotic behavior had long been associated with nonlinear systems, but not with such simple systems. The behavior seemed, in essence, random, but there is no randomness at all in the equations: they are fully deterministic.** Thus, this characteristic later became known as deterministic chaos.
Lorenz looked at the behavior of the solutions by drawing graphs of pairs of the dynamical variables as time progressed. The resulting paths are known as the system’s trajectory in phase space. The trajectory for his set of equations looped around on two different spirals, never settling down to a single line and shifting sides from one spiral to the other at unpredictable intervals. (See this image for a beautiful example that illustrates these ideas.) The image above shows how the trajectory looks, seen in quasi-3D. (Follow the strings of dots as they swoop about one loop and then fly to the other side.)
These phase-space trajectories where unlike anything seen before. Usually a trajectory would settle down into an orbit that, after some time had passed, would never change, or maybe the orbit would decay and just settle into a point where it would stay forever. Think of a coin rolling around on its side on the floor: after awhile the coin flops over and just sits on the floor in one spot forever after.
There was another oddity, too, in these phase-space trajectories Lorenz plotted. Dynamical systems that are deterministic have trajectories in phase space that never cross themselves–it’s just the way the mathematics works. However, Lorenz’ trajectories did appear to cross themselves and yet, to speak loosely, they never got tangled up. The best he could say at the time was that the planes that the trajectories were in seemed, somehow, like an infinitely thin stack of planes that kept the trajectories apart, or something.
He published his results in the March, 1963 issue of the Journal of the Atmospheric Sciences; you can download the paper online from this page, which has the abstract of the paper on it. If you look at the paper you might see that Lorenz simply didn’t have the vocabulary at the time to talk about the behavior of this system. All of that was developed about a decade later. Very few people saw his original paper and it had little impact until it was rediscovered c. 1970.
These points or orbits in phase space that are the long-time trajectories of dynamical systems are known as the attractors in the phase space, for rather obvious reasons. The Lorenz Attractor, as it became know, was an altogether stranger fish than those normal attractors. As part of the rediscovery of Lorenz’ work, in a famous and highly unreadable paper by David Ruelle and Floris Takens (“On the nature of turbulence”, Communications of Mathematical Physics 20: 167-192; 1971) the term strange attractor was created to describe such dynamical oddities of deterministic chaos as the Lorenz Attractor.##
Strange attractors have had quite the vogue, as has deterministic chaos in dynamical systems. The characteristic feature of deterministic chaos, in addition to its unpredictability, is its extreme sensitivity to initial conditions.&& Also in the seventies Benoit Mandelbrot’s work on fractals began to enter the mathematical-physics consciousness and the concepts developed that allowed strange attractors to be described as having non-integer dimensions in phase space. The dimension of the Lorenz Attractor is about 2.06, so it’s almost but not quite flat or, alternatively, it’s the “thick” plane that Lorenz originally conceptualized.
Lorenz has contributed to the popular culture, but few people are aware of it. His original interest was in modeling the atmosphere in the context of weather forecasting. His discovery of the Lorenz attractor and deterministic chaos (albeit not called that at the time) made it suddenly apparent that there were probably limits to how long the “long” in “long-term forecasting” could be. As he put it in the abstract to his paper, “The feasibility of very-long-range weather prediction is examined in the light of these results.” Very understated! There’s no direct calculation of the time involved–it’s probably impossible, or nearly so–but it’s generally thought that good forecasts don’t go much beyond three days. Check your own five-day forecasts for accuracy and you’ll start to see just how often things go awry around day five. The point here is that weather models are very good but there are fundamental limitations on forecasting because of the system’s extreme sensitivity to initial conditions.††
If you’ve been reading the footnotes, you already know that Lorenz gave a paper at a AAAS meeting in 1972 titled “Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas?” And that’s how the extreme sensitivity to initial conditions of systems exhibiting deterministic chaos became known as “the butterfly effect”.
For pretty good reasons, many people are fascinated by creating images of the Lorenz Attractor. Among other reasons it seems infinitely variable and, well, so strange. This Google images search for “Lorenz attractor” can get you started on that exploration.
———-
† This is my source page for the image, which itself has an interesting history. It was rendered by Paul Bourke, who has a gallery featuring many beautiful images of fractals and strange attractors and related objects, of which this is just one example.
* Some obituaries:
Finally, Bob Park had this to say:
EDWARD N. LORENZ: THE FATHER OF CHAOS THEORY.
A meteorologist, Lorenz died Wednesday at 90. He found that seemingly insignificant differences in initial conditions can lead to wildly divergent outcomes of complex systems far down the road. At a AAAS meeting in 1972, the title of his talk asked “Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas.” Alas, the frequency of storms cannot be reduced by killing butterflies.
[Robert L. Park, What's New, 18 April 2008.]
‡ The equation set is derived from the full set of equations that describe Rayleigh-Bénard convection, which is thermally driven convection in a layer of fluid heated from below. In my early graduate-school days I did some research on the topic, which may explain my early interest in chaos and related topics.
# A “space” is quite a general thing and could be made up of any n variables and thereby be an “n-space”. However, the phrase “phase space” is generally reserved for n-spaces in which the n variables are specifically the variables found in the dynamical equations that define the dynamical system of interest. For present purposes, this footnote is entirely optional.
** Deterministic here means pretty much what one thinks it would mean, but more specifically it means being single-valued in the time variable, or, equivalently, that the solutions of the equations reverse themselves if time is run backwards. Virtually all real dynamical systems are invariant under time reversal.
## I tried to read part of the paper once. I remember two things about it. One was that they said the paper was divided into two sections, the first more popular in development, the second more mathematical; I couldn’t get past the first page of the first section. But I also remember how they developed some characteristics of these attractors, which seemed very peculiar at the time, and then they simply said: “We shall call such attractors ‘strange’.” Et voilà!
&& Also expressed as exponential divergence of phase-space trajectories.
†† The Met–the UK Meteorological Office–has an interesting series of pages about how weather forecasting works in practice, starting at “Ensemble Prediction“. The Lorenz attractor appears on the second page of that series, called “The Concept of Ensemble“.
Mar
31
Posted by jns on 31 March 2008
Here’s an unexpected bit of innumeracy.
I’m about to finish up a book by Colin Tudge called The Time Before History : A Million Years of Human Impact (New York : Scribner, 1996; 366 pages). I expect there will be a book note soonish.
Anyway, here are two quotations from two nearby pages. See if you spot the problem.
We know, too, as related in chapter 2, that when the ice ages ended, they could, in any one place, end fast. Twenty years could see a 7°C (44°F) rise in temperature; the difference between a frozen landscape and a temperate one. [p. 301]
Besides, at the trough of the last ice age, 18,000 years ago, the surface of the sea in the eastern Mediterranean is known to have cooled by more than 6°C (43°F), which in ecological terms is huge, and yet the elephants and their miniaturized neighbors came through those harsh times. [p. 302]
Your reaction may be different, but the author’s–or editor’s!–error in converting the temperature differences from Celsius to Fahrenheit stands out to me as though written in flashing neon. Could they really believe that the temperature of the Mediterranean had changed by an amazing 43°F? “Huge” is one thing, but that’s huge!
Not so long ago I wrote at excessive length about how to convert values on one temperature scale to values on the other. What I didn’t talk about was how to compare temperature differences.
Look again at the formula for converting Celsius temperatures to Fahrenheit temperatures:
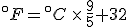
If we talk a bit about this equation, there are two things that it is telling us:
- That Celsius degrees are bigger, nine-fifths bigger, than Fahrenheit degrees, which means that it takes fewer Celsius degrees to express a temperature change than Fahrenheit degrees; and
- That the zero points on the two scales are offset by 32°F.
But this equation and this explanation refer to converting temperature values on one scale to the other. If we want to talk about temperature differences, that’s another matter, and that’s why it’s good to talk/think about what the equation above is saying.
Suppose we have two temperature values specified on the Celsius scale; call them 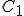 and
and 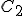 . Then, to find the corresponding temperature difference expressed in terms of Fahrenheit degrees, we need to write down these two equations:
. Then, to find the corresponding temperature difference expressed in terms of Fahrenheit degrees, we need to write down these two equations:
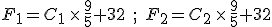
and then subtract one from the other. Do the algebra and you find
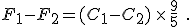
You’ll notice that the offset value of 32 disappears when you do the subtraction. This is as we expected because we had just talked about how Celsius degrees are nine-fifths bigger than Fahrenheit degrees.
But now you can see the error made by the author or his editor: they erroneously used the equation to convert temperatures on the Celsius scale to temperatures on the Fahrenheit scale, rather than merely change a temperature difference from degrees of one size to degrees of another size.
The innumeracy aspect is that, before using the conversion equation, one should know what it is saying. This simple step would alert anyone that 6°C could never be 43°F. Knowing that Celsius degrees are nine-fifths bigger than Fahrenheit degrees let’s us write the correct values for these temperature differences immediately:
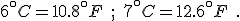
Mar
28
Posted by jns on 28 March 2008
A recent story from Science@NASA (“Spring is Aurora Season“, 20 March 2008) told an interesting story about how the aurora borealis seems to be more active near the equinoxes. The apparent reason has to do with “magnetic tubes” whose creation is favored when the Earth’s magnetic poles have the alignment relative to the Sun that they exhibit around the equinoxes.
Fine. Very interesting. But who could possibly pay attention to that when this was the image illustrating the article?

This stunning photograph (reduced to fit in this column better) was taken on 1 March 2008 in Tomso, Norway by photographer Bjørn Jørgensen.
His website is called “Arctic Photo” (direct to the English version).
Now, go ahead and give me one good reason why you would not want to click over to his site and see the beautiful photographs of the aurora borealis, not to mention sections like “The Sun at Night”, “Traditional Boatbuilding”, and “North Norway Winter” in his portfolio?
Mar
27
Posted by jns on 27 March 2008
Back in the days when we roamed at video stores looking for something that might pique my interest, my attention would invariably be drawn to any movie that reviewers blurbed as–and publicists dared print on the package–”quirky”. So, when my eyes landed on Scott Huler’s Defining the Wind : The Beaufort Scale, and How a Nineteenth-Century Admiral Turned Science into Poetry (New York : Crown Publishers, 2004, 290 pages), it looked guaranteed to be quirky. I grabbed it.
As I expected I enjoyed it. What I hadn’t expected was to enjoy it quite so much as I did. The subject is indeed odd, the style idiosyncratic, the topics covered diverse and wide-ranging, but in Huler’s hands it all adds up to a delightful and informative adventure of research and discovery that the author shares vividly with the reader in an unexpectedly intimate way.
Huler is not a scientist but his approach to discovering and understanding the times and circumstances surrounding the creation of Beaufort’s Scale is remarkably scientific; he is aware of this and seems to ascribe it to an awakening of a high-definition awareness of the natural world that resulted from spending so much time contemplating the Beaufort Scale. All this makes the book itself a thing of high scienticity; reading it is to hone one’s intuition about how science actually works.
In fact, the book is akin to what the author came to call a Beaufort Moment: “A Beaufort moment is any moment where instead of merely passing through my surroundings I notice them, notice them in a way that engenders understanding. [p. 242]” I loved this realization that he described late in the book, the summation of his experience as it transcended a mere research project:
And that is what I finally figured out the Beaufort Scale was trying to tell me. The Beaufort Scale is about paying attention. It’s about noticing whether smoke rises vertically or drifts, whether it’s the leaves shaking or the whole branches, whether your umbrella turns inside out or just rattles around some. More, it’s about taking note of those details, filing them away, in memory or, as the Manual of Scientific Enquiry would have it, in the notebook you’d never leave the house without (along, of course, with your pencil and your map and compass). It’s about being able to express what you’ve seen simply and clearly, in as few words as possible, so that others can share it. It’s about the good of sharing that knowledge, of everyone paying attention so that, together, we can all learn as much as possible.
The Beaufort Scale is a manual, a guide for living. It’s like a cross between the Boy Scout Handbook and the Old Farmer’s Almanac: a bunch of cool information that you’ll never be sorry you have, and a general policy of being prepared to deal with it: to notice that information and share it for the good of everybody involved. It’s a philosophy of attentiveness, a religion based on observation: an entire ethos in 110 words. One hundred ten words, that is, and four centuries of backstory. [pp. 237—238]
If, by the way, you need to see a version of the Scale to see what he refers to by the “110 words”, this version from the [UK] Meteorological Office comes the closest to Huler’s original inspiration. (After you’ve read the book you’ll appreciate the futility of trying to define the Beaufort Scale.) Personally, I think my favorite phrase is “umbrellas used with difficulty” (which is, therefore, how I know that the stormy afternoon when I arrived in New York City a few weeks ago was accompanied by Beaufort Scale 6 winds of roughly 25-30 mph).
It’s a book I can recommend most heartily to non-scientists and scientists alike; everyone is certain to find plenty to stimulate their thoughts and refine their perceptions of the natural world.
Mar
27
Posted by jns on 27 March 2008
When I went recently on my cultural trip to New York with Bill, I traveled with a couple of books: reading for the train trip and for those quiet moments at the hotel. One of the books I took was John H. Lienhard’s Inventing Modern : Growing up with X-Rays, Skyscrapers, and Tailfins (Oxford : Oxford University Press, 2003. 292+ix pages). Fortunately I started reading first thing on the train, and I made sure there were enough quiet moments at the hotel for me to finish the book in a couple of days. What a page turner! My book note is here.
Lienhard observes that in the early part of the 20th Century there was a feeling of Modern. It was something more than just modern, more than just new technology or new science–there was some indefinable spirit of adventure, feeling of invention, and optimistic attitude that seemed to dominate American culture. Naturally, given something indefinable like Modern, Lienhard set out to define it.
Lienhard, Anderson Professor of Technology and Culture, Emeritus, at the University of Houston was there for much of the Modern adventure, and his first-hand experiences adds heft to his discussion of the ideas, technology, and cultural currents of the time that met up in Modern.
I had previously read his book How Invention Begins, which impressed me very much, so I was excited to start on this one and I wasn’t disappointed. I did think that Invention had more profound insights on offer, but that doesn’t mean that Inventing Modern was an intellectual lightweight, although its tone was much more personal and somewhat more casual. They are both eminently readable and thoughtful and stimulating, but likely to stimulate different trains of thought.
I admit that there was an extra little frisson from reading about the nearby Empire State Building, which we could see from the street in front of our hotel, and the Chrysler Building, which we could see from the Brooklyn Bridge and which we visited one day. I’m certain however, that readers can enjoy the book without being in Manhattan to read it.
Feb
29
Posted by jns on 29 February 2008
Bob Park seems reinvigorated by all the science-silliness and some non-silliness going on that he reports in the latest (29 February) edition of “What’s New“. (Subscription information here.) Between feeling lazy and amused, I decided to include it all!
1. FENCES: SOMETHING THERE IS THAT DOESN’T LOVE A WALL.
Technology makes us arrogant. A 28-mile pilot project for a high-tech “virtual fence” south of Tucson, which cost $100M, is now acknowledged to be a failure. The history of the world is a story of fences that failed: the Great Wall of China, the Red Sea, the Berlin Wall, Robert McNamara’s electronic wall dividing Vietnam, followed by the horror of Agent Orange. Securing the 2,000 mile border was expected to cost $7.6B; the estimate will now go up. But desperate people will find a way in spite of obstacles. By contrast, the border with Canada remains unsecured. Why would Canadians want to come here? About 200,000 illegal immigrants enter from Mexico each year. For $7.6B we could pay them $38,000 each to stay in Mexico. We would all be better off.
2. EVOLUTION: THE GOOD NEWS IS FROM FLORIDA.
Last week WN reported the happy news that the Board of Education had approved science standards that call for teaching “the scientific theory of evolution.” As Harold Kroto, 1996 Nobel Prize and professor of chemistry at Florida State, put it, “The phrase ‘scientific theory’ gives us the leverage to differentiate between theories that are supported by evidence and those that aren’t.” It also pleased a conservative legislator who was happy it wasn’t called a “scientific fact.” Scientists should make it a point to distinguish between “scientific theory” and biblical revelation, which is “not even a theory.” It never ends; legislation is now being considered that would allow criticisms of evolution to be taught.
3. CREATIONISM: THE BAD NEWS IS FROM TEXAS.
A strong editorial in today’s issue of Nature warns that the Institute for Creation Research (ICR), which moved from San Diego to Dallas last year, has applied to the Texas Higher Education Coordinating Board for the right to grant online master’s degrees in science education. An advisory board has recommended acceptance. Founded by Henry Morris in 1972, the ICR regards the Bible as an inerrant source of scientific and historical fact. The Board had been expected to vote on the application in January, but requested additional information. The vote is now expected at the boards 24 April meeting. Steven Weinberg, Physics Nobel 1979, who five years ago defended the rights of Texas school children to learn the natural laws that govern our existence http://bobpark.physics.umd.edu/WN03/wn091903.html , has urged the board to deny accreditation to the Creation Research Institute. Every Texas scientist should do the same.
4. PEW FORUM: THE U.S. RELIGIOUS LANDSCAPE.
Based on interviews with more than 35,000 Americans age 18 and older, the Pew survey finds a changing landscape. More than a quarter of Americans have left the faith they were born in. Americans who are unaffiliated with any religion have seen the greatest growth in numbers as a result. Catholicism has experienced the greatest net losses. Is there any indication that Americans are becoming more rational? Perhaps. About a fourth of those who are unaffiliated describe themselves as atheist or agnostic.
Feb
27
Posted by jns on 27 February 2008
After Copernicus published De Revolutionibus in 1543, acceptance of the idea that the Earth orbited the Sun was neither immediate nor universal. Some appealed to common sense:
No one in his senses, or imbued with the slightest knowledge of physics will ever think that the earth, heavy and unwieldy from its own weight and mass, staggers up and down around its own centre and that of the sun; for at the slightest jar of the earth, we would see cities and fortresses, towns and mountains thrown down.
– Jean Bodin (1529–1596), quoted in Peter Watson, Ideas, (New York : HarperCollins, 2005), p. 517
Isn’t it interesting how some common sense becomes uncommon.
Feb
24
Posted by jns on 24 February 2008
 This week’s beard belongs to Albrecht Dürer, easily in my top-10 of most extraordinary artists ever. This amazing self-portrait was painted when the artist was 29 years old, in the year 1500. Is it symbolic that Dürer paints himself in this remarkably self-possessed, self-confident pose, looking directly at the viewer? It’s also interesting that he paints himself more as an aristocrat rather than with the commonly affected palette in hand, as a painter. What is the power in this painting that makes it feel so much as though it communicates directly with the viewer across the more than five centuries since Dürer painted it. Honestly, it creates for me a frisson that very few works of art manage to do.
This week’s beard belongs to Albrecht Dürer, easily in my top-10 of most extraordinary artists ever. This amazing self-portrait was painted when the artist was 29 years old, in the year 1500. Is it symbolic that Dürer paints himself in this remarkably self-possessed, self-confident pose, looking directly at the viewer? It’s also interesting that he paints himself more as an aristocrat rather than with the commonly affected palette in hand, as a painter. What is the power in this painting that makes it feel so much as though it communicates directly with the viewer across the more than five centuries since Dürer painted it. Honestly, it creates for me a frisson that very few works of art manage to do.
Dürer was born in Nuremberg, Germany in 1471 (21 May), and he died in Nuremberg, Germany in 1528 (6 April). He did not stay his entire life in Nuremberg, but it seems that it was his center and he returned there after his various excursions to Italy and the Netherlands. He was a master of drawing, painting, printmaking, and engraving. He helped develop the newly emerging technique of perspective. He died relatively wealthy, apparently making his money from his prints, for which he was justly celebrated across Europe. (The Wikipedia biography of Dürer is nicely done; I also enjoyed the biography and the lovely images of stamps featuring works by Dürer on this page from Art History on Stamps.)
This page from WebMuseum, Paris has a nice collection of images, some biography, and a useful discussion of his portraiture. I don’t see much point in trying to name any particular favorites, although this self-portrait I certainly put on his list of masterworks. Also famous, and for good reason, are his smallish, early watercolors “A Young Hare” and “The Large Turf“. Both are breathtaking in their amazing realism, yet they go beyond mere realism and seem to breathe with a vitality beyond what any photograph could conjure for these subjects.
When we were in Rome in 2001, we happened upon a small exhibit concerning prints and printmaking through history, and there we saw some Dürer first hand. There was a copy of his notorious print of a Rhinoceros (notorious for being notably inaccurate, apparently drawn from a verbal description of the first rhino to arrive in Europe). We also saw two amazing “oversized” woodcuts (describing them as “oversized” seems such an understatement!) “The Triumphal Arch and the Large Triumphal Carriage of Maximilian I”, which are discussed at some length, along with some remarkable photographs of the works, on this page.
Seeing these things first hand was quite an experience that still feels very close to me.
 The image at right is a gorgeous rendering† of a mystifying object known as the Lorenz Attractor. It shares its name with Edward Lorenz, its discoverer, who died earlier this month at the age of 90.* Edward Lorenz is sometimes called “the father of chaos”, and the Lorenz attractor is the reason.
The image at right is a gorgeous rendering† of a mystifying object known as the Lorenz Attractor. It shares its name with Edward Lorenz, its discoverer, who died earlier this month at the age of 90.* Edward Lorenz is sometimes called “the father of chaos”, and the Lorenz attractor is the reason. 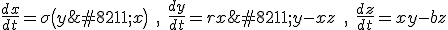
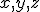 , by the way, are not spatial variables but instead more abstract variables that represent wind velocity, pressure, and temperature in the atmosphere. You can still think of them, though, as the three dimensions of an abstract “space” that is referred to as “phase space”.# The
, by the way, are not spatial variables but instead more abstract variables that represent wind velocity, pressure, and temperature in the atmosphere. You can still think of them, though, as the three dimensions of an abstract “space” that is referred to as “phase space”.# The 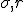 and
and 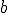 are parameters in the system, numbers that get set to some value and then left at that value; parameters allow the set of equations to describe a whole family of dynamical systems.
are parameters in the system, numbers that get set to some value and then left at that value; parameters allow the set of equations to describe a whole family of dynamical systems. 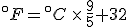
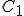 and
and 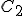 . Then, to find the corresponding temperature difference expressed in terms of Fahrenheit degrees, we need to write down these two equations:
. Then, to find the corresponding temperature difference expressed in terms of Fahrenheit degrees, we need to write down these two equations: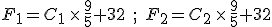
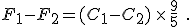
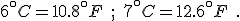

 This week’s beard belongs to Albrecht Dürer, easily in my top-10 of most extraordinary artists ever. This amazing self-portrait was painted when the artist was 29 years old, in the year 1500. Is it symbolic that Dürer paints himself in this remarkably self-possessed, self-confident pose, looking directly at the viewer? It’s also interesting that he paints himself more as an aristocrat rather than with the commonly affected palette in hand, as a painter. What is the power in this painting that makes it feel so much as though it communicates directly with the viewer across the more than five centuries since Dürer painted it. Honestly, it creates for me a frisson that very few works of art manage to do.
This week’s beard belongs to Albrecht Dürer, easily in my top-10 of most extraordinary artists ever. This amazing self-portrait was painted when the artist was 29 years old, in the year 1500. Is it symbolic that Dürer paints himself in this remarkably self-possessed, self-confident pose, looking directly at the viewer? It’s also interesting that he paints himself more as an aristocrat rather than with the commonly affected palette in hand, as a painter. What is the power in this painting that makes it feel so much as though it communicates directly with the viewer across the more than five centuries since Dürer painted it. Honestly, it creates for me a frisson that very few works of art manage to do.