Edward Lorenz and His Butterflies

Posted by jns on 30 April 2008

The image at right is a gorgeous rendering^† of a mystifying object known as the Lorenz Attractor. It shares its name with Edward Lorenz, its discoverer, who died earlier this month at the age of 90.^* Edward Lorenz is sometimes called “the father of chaos”, and the Lorenz attractor is the reason.

Lorenz was a mathematician and meteorologist. In the early 1960s he was using what is usually described as an “extremely primitive computer” (a “Royal McBee LPG-30″) to work out some numerical solutions to a relatively simple set of equations he was using to model atmospheric convection^‡. They are a simple set of differential equations, not particularly scary, so we might as well see what they look like:

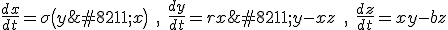
The 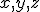, by the way, are not spatial variables but instead more abstract variables that represent wind velocity, pressure, and temperature in the atmosphere. You can still think of them, though, as the three dimensions of an abstract “space” that is referred to as “phase space”.^# The 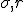and 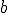are parameters in the system, numbers that get set to some value and then left at that value; parameters allow the set of equations to describe a whole family of dynamical systems.

What happened next (in the dramatic flow of time) is a story that’s been told over and over. Here’s how the American Physical Society tells it:

He [Lorenz] kept a continuous simulation running on an extremely primitive computer [!], which would produce a day’s worth of virtual weather every minute. The system was quite successful at producing data that resembled naturally occurring weather patterns: nothing ever happened the same way twice, but there was clearly an underlying order.

One day in the winter of 1961, Lorenz wanted to examine one particular sequence at greater length, but he took a shortcut. Instead of starting the whole run over, he started midway through, typing the numbers straight from the earlier printout to give the machine its initial conditions. Then he walked down the hall for a cup of coffee, and when he returned an hour later, he found an unexpected result. Instead of exactly duplicating the earlier run, the new printout showed the virtual weather diverging so rapidly from the previous pattern that, within just a few virtual “months”, all resemblance between the two had disappeared.

At first Lorenz assumed that a vacuum tube had gone bad in his computer, a Royal McBee, which was extremely slow and crude by today’s standards. Much to his surprise, there had been no malfunction. The problem lay in the numbers he had typed. Six decimal places were stored in the computer’s memory: .506127. To save space on the printout, only three appeared: .506. Lorenz had entered the shorter, rounded-off numbers assuming that the difference [of] one part in a thousand was inconsequential.

["This Month in Physics History: 'Circa January 1961: Lorenz and the Butterfly Effect' ", APS News, January 2003.]

This was a shocking result. The system of equations he was studying was nonlinear, and it is well-known that nonlinear systems can amplify small differences — Lorenz did not discover nonlinear amplification as some have written. But this divergence of the solutions was extreme: after not much time the two solutions not only weren’t close, they were so far apart that it looked like they never had anything to do with each other. This is a characteristic known as extreme sensitivity to initial conditions.

What’s more, one could put in virtually identical initial conditions all day long and keep getting different results a little ways down the road. In fact, the state of the system at these later times was unpredictable in practical terms — the system was chaotic in behavior.

That chaotic behavior was shocking result number two. Chaotic behavior had long been associated with nonlinear systems, but not with such simple systems. The behavior seemed, in essence, random, but there is no randomness at all in the equations: they are fully deterministic.^** Thus, this characteristic later became known as deterministic chaos.

Lorenz looked at the behavior of the solutions by drawing graphs of pairs of the dynamical variables as time progressed. The resulting paths are known as the system’s trajectory in phase space. The trajectory for his set of equations looped around on two different spirals, never settling down to a single line and shifting sides from one spiral to the other at unpredictable intervals. (See this image for a beautiful example that illustrates these ideas.) The image above shows how the trajectory looks, seen in quasi-3D. (Follow the strings of dots as they swoop about one loop and then fly to the other side.)

These phase-space trajectories where unlike anything seen before. Usually a trajectory would settle down into an orbit that, after some time had passed, would never change, or maybe the orbit would decay and just settle into a point where it would stay forever. Think of a coin rolling around on its side on the floor: after awhile the coin flops over and just sits on the floor in one spot forever after.

There was another oddity, too, in these phase-space trajectories Lorenz plotted. Dynamical systems that are deterministic have trajectories in phase space that never cross themselves–it’s just the way the mathematics works. However, Lorenz’ trajectories did appear to cross themselves and yet, to speak loosely, they never got tangled up. The best he could say at the time was that the planes that the trajectories were in seemed, somehow, like an infinitely thin stack of planes that kept the trajectories apart, or something.

He published his results in the March, 1963 issue of the Journal of the Atmospheric Sciences; you can download the paper online from this page, which has the abstract of the paper on it. If you look at the paper you might see that Lorenz simply didn’t have the vocabulary at the time to talk about the behavior of this system. All of that was developed about a decade later. Very few people saw his original paper and it had little impact until it was rediscovered c. 1970.

These points or orbits in phase space that are the long-time trajectories of dynamical systems are known as the attractors in the phase space, for rather obvious reasons. The Lorenz Attractor, as it became know, was an altogether stranger fish than those normal attractors. As part of the rediscovery of Lorenz’ work, in a famous and highly unreadable paper by David Ruelle and Floris Takens (“On the nature of turbulence”, Communications of Mathematical Physics 20: 167-192; 1971) the term strange attractor was created to describe such dynamical oddities of deterministic chaos as the Lorenz Attractor.^##

Strange attractors have had quite the vogue, as has deterministic chaos in dynamical systems. The characteristic feature of deterministic chaos, in addition to its unpredictability, is its extreme sensitivity to initial conditions.^&& Also in the seventies Benoit Mandelbrot’s work on fractals began to enter the mathematical-physics consciousness and the concepts developed that allowed strange attractors to be described as having non-integer dimensions in phase space. The dimension of the Lorenz Attractor is about 2.06, so it’s almost but not quite flat or, alternatively, it’s the “thick” plane that Lorenz originally conceptualized.

Lorenz has contributed to the popular culture, but few people are aware of it. His original interest was in modeling the atmosphere in the context of weather forecasting. His discovery of the Lorenz attractor and deterministic chaos (albeit not called that at the time) made it suddenly apparent that there were probably limits to how long the “long” in “long-term forecasting” could be. As he put it in the abstract to his paper, “The feasibility of very-long-range weather prediction is examined in the light of these results.” Very understated! There’s no direct calculation of the time involved–it’s probably impossible, or nearly so–but it’s generally thought that good forecasts don’t go much beyond three days. Check your own five-day forecasts for accuracy and you’ll start to see just how often things go awry around day five. The point here is that weather models are very good but there are fundamental limitations on forecasting because of the system’s extreme sensitivity to initial conditions.^††

If you’ve been reading the footnotes, you already know that Lorenz gave a paper at a AAAS meeting in 1972 titled “Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas?” And that’s how the extreme sensitivity to initial conditions of systems exhibiting deterministic chaos became known as “the butterfly effect”.

For pretty good reasons, many people are fascinated by creating images of the Lorenz Attractor. Among other reasons it seems infinitely variable and, well, so strange. This Google images search for “Lorenz attractor” can get you started on that exploration.
———-
^† This is my source page for the image, which itself has an interesting history. It was rendered by Paul Bourke, who has a gallery featuring many beautiful images of fractals and strange attractors and related objects, of which this is just one example.

^* Some obituaries:

• Telegraph [UK]
• Wired
• New York Times

Finally, Bob Park had this to say:

EDWARD N. LORENZ: THE FATHER OF CHAOS THEORY.
A meteorologist, Lorenz died Wednesday at 90. He found that seemingly insignificant differences in initial conditions can lead to wildly divergent outcomes of complex systems far down the road. At a AAAS meeting in 1972, the title of his talk asked “Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas.” Alas, the frequency of storms cannot be reduced by killing butterflies.

[Robert L. Park, What's New, 18 April 2008.]

^‡ The equation set is derived from the full set of equations that describe Rayleigh-Bénard convection, which is thermally driven convection in a layer of fluid heated from below. In my early graduate-school days I did some research on the topic, which may explain my early interest in chaos and related topics.

^# A “space” is quite a general thing and could be made up of any n variables and thereby be an “n-space”. However, the phrase “phase space” is generally reserved for n-spaces in which the n variables are specifically the variables found in the dynamical equations that define the dynamical system of interest. For present purposes, this footnote is entirely optional.

^** Deterministic here means pretty much what one thinks it would mean, but more specifically it means being single-valued in the time variable, or, equivalently, that the solutions of the equations reverse themselves if time is run backwards. Virtually all real dynamical systems are invariant under time reversal.

^## I tried to read part of the paper once. I remember two things about it. One was that they said the paper was divided into two sections, the first more popular in development, the second more mathematical; I couldn’t get past the first page of the first section. But I also remember how they developed some characteristics of these attractors, which seemed very peculiar at the time, and then they simply said: “We shall call such attractors ‘strange’.” Et voilà!

^&& Also expressed as exponential divergence of phase-space trajectories.

^†† The Met–the UK Meteorological Office–has an interesting series of pages about how weather forecasting works in practice, starting at “Ensemble Prediction“. The Lorenz attractor appears on the second page of that series, called “The Concept of Ensemble“.