Archive for the ‘Scientists & History’ Category
Jul
07
Posted by jns on
July 7, 2008
This is geneticist and cellist Edmund Beecher Wilson (1856–1939). On the Columbia University Website, where he is one of their “Living Legacies” (despite his being deceased these last 70 years), he is hailed as the first “cell biologist”, with which history seems agreeable. He spent the bulk of his career at that institution. That “living Legacies” article, “Edmund Beecher Wilson: America’s First Cell Biologist“, by Qais Al-Awqati, is a good appreciation of E.B.Wilson’s work and life, and the source of these two photographs of the younger Wilson.
Early in his research life, just after getting his Ph.D. from Johns Hopkins, Wilson became interested in studying the connection between evolution and phylogeny, or phylogenetics (the course of evolution of a species). Later he moved into cell biology and made his greatest discoveries through careful and detailed observation of cell divisions during development, starting with the first division after fertilization of an egg cell by a sperm cell. His work set the course for genetics: the discovery of chromosomes, his own discovery that X and Y chromosomes determine sex (gender), which was a controversial finding at the time, and integrating Mendelian patterns of inheritance into genetics (which wasn’t quite genetics at the time, of course).
Some of this I knew about because I recently finished reading In Pursuit of the Gene : From Darwin to DNA (Cambridge, MA : Harvard University Press 2008) by James Schwartz. I liked the book very much, predominantly for these two reasons: 1) it was a thoroughly researched history of the idea of the gene and how it evolved from its earliest (and rather strange) germ of an idea in the theories of Darwin; and 2) author Schwartz actually discussed experiments and their results as a way to comprehend how the idea of the gene made its perilous journey to the modern idea that everyone recognizes and takes for granted. Of course, I wrote a book note.
Even though Schwartz took a biographical approach to telling his story, which he could do largely because the gene-meme almost moved from person to person, as though stepping across a stream on stones, the biographical material were there to serve his main story, that of the idea of the gene. One thing that I did not pick up from Schwartz’ book was Wilson’s love of music, nor the fact that he was a fellow cellist. This is from Qais Al-Awqati’s piece (linked above):
It seems that everybody in Wilson’s family played an instrument. His father played the violin and cello, his mother and sister played the piano (as did both of his aunts), and his brother Charles was a violinist. Wilson began by taking singing lessons, and although he did not have a good singing voice, he says that these lessons left him “with an inveterate habit of reading all of music in do re mi language.” He learned to play the flute, but when he went to Johns Hopkins, he developed a lifelong passion for playing the cello. He wrote, “I was too old to take up so difficult an instrument with any hope of mastering it.” But he eventually became an accomplished cellist and reveled in playing quartets in Bryn Mawr, Philadelphia, and New York.
What a treat: a cute, bearded scientist who was also a cellist! I feel a strange connection across the decades.
Jun
30
Posted by jns on
June 30, 2008
 This is chemist Richard Willstätter. I confess that his name was not familiar to me despite his having won the 1915 Nobel Prize in chemistry.
This is chemist Richard Willstätter. I confess that his name was not familiar to me despite his having won the 1915 Nobel Prize in chemistry.
Here are two short excerpts from his Nobel biography that summarize his prize-winning research.
As a young man he studied [c. 1902] principally the structure and synthesis of plant alkaloids such as atropine and cocaine. In this, as in his later work on quinone and quinone type compounds which are the basis of many dyestuffs, he sought to acquire skill in chemical methods in order to prepare himself for the extensive and more difficult work of investigating plant and animal pigments. [From Munich he went to work in Switzerland for seven years, returning to Germany in 1912, where he took up a position in a newly established Institute of Chemistry in Berlin/Dahlem.]
In the two short years before the outbreak of the first World War he was able with a team of collaborators to round off his investigations into chlorophyll and, in connexion with that, to complete some work on haemoglobin and, in rapid succession, to carry out his studies of anthocyanes, the colouring matter of flowers and fruits. These investigations into plant pigments, especially the work on chlorophyll, were honoured by the award of the Nobel Prize for Chemistry (1915)….
His main achievement, according to the Nobel presentation, was elucidating the chemical nature of the chlorophyll and “having been the first to recognize and to prove with complete evidence the fact that magnesium is not an impurity, but is an integral part of the native, pure chlorophyll – a fact of high importance from the biological point of view (source, the rest of which makes for very interesting reading).” By the way, “Plant Pigments” was the title of Willstätter’s Nobel lecture.
He continued to be productive after winning the prize and worked until he chose to end his career in what must have seemed a startling move.
Willstätter’s career came to a tragic end when, as a gesture against increasing antisemitism, he announced his retirement in 1924. Expressions of confidence by the Faculty, by his students and by the Minister failed to shake the fifty-three year old scientist in his decision to resign. He lived on in retirement in Munich, maintaining contact only with those of his pupils who remained in the Institute and with his successor, Heinrich Wieland, whom he had nominated. Dazzling offers both at home and abroad were alike rejected by him. In 1938 he fled from the Gestapo with the help of his pupil A. Stoll and managed to emigrate to Switzerland, losing all but a meagre part of his belongings.
He lived in Switzerland until he died on 3 August 1942, of a heart attack. I was interested to read that a memorial to Willstätter was unveiled in Muroalto, where he lived his last years, in 1956, the year I was born.
This portrait photograph (source) was taken in 1942 by an unidentified photographer. And now we come to the original reason that Willstätter is the subject of this post, namely so that I could mention that the Smithsonian Institution’s Dibner Library of the History of Science and Technology has put some of their large collection of portraits of scientists and inventors online at Flickr: “Portraits of Scientists and Inventors“. This collection has 144 portraits; they tell us that the entire collection is available online in the “Scientific Identity” digital collection.
I first read about the Smithsonian Library’s adding photographs to the Flickr commons project by reading an entry in the Smithsonian Library’s blog. It wasn’t long ago that the Library of Congress delighted fans of photography by putting big chunks of their collections on Flickr in a first-of-its-kind collaboration.
It’s a lot of fun with wonderful images to see; it’s also a great sink of one’s time. But this is culture and heritage and history, right? Besides, I think we’re all better people for knowing more about Richard Willstätter now. What a learning experience is Beard of the Week!
I expect we’ll be exploring more of these portraits in the future.
Apr
30
Posted by jns on
April 30, 2008
 The image at right is a gorgeous rendering† of a mystifying object known as the Lorenz Attractor. It shares its name with Edward Lorenz, its discoverer, who died earlier this month at the age of 90.* Edward Lorenz is sometimes called “the father of chaos”, and the Lorenz attractor is the reason.
The image at right is a gorgeous rendering† of a mystifying object known as the Lorenz Attractor. It shares its name with Edward Lorenz, its discoverer, who died earlier this month at the age of 90.* Edward Lorenz is sometimes called “the father of chaos”, and the Lorenz attractor is the reason.
Lorenz was a mathematician and meteorologist. In the early 1960s he was using what is usually described as an “extremely primitive computer” (a “Royal McBee LPG-30″) to work out some numerical solutions to a relatively simple set of equations he was using to model atmospheric convection‡. They are a simple set of differential equations, not particularly scary, so we might as well see what they look like:
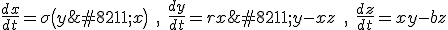
The 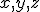 , by the way, are not spatial variables but instead more abstract variables that represent wind velocity, pressure, and temperature in the atmosphere. You can still think of them, though, as the three dimensions of an abstract “space” that is referred to as “phase space”.# The
, by the way, are not spatial variables but instead more abstract variables that represent wind velocity, pressure, and temperature in the atmosphere. You can still think of them, though, as the three dimensions of an abstract “space” that is referred to as “phase space”.# The 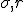 and
and 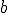 are parameters in the system, numbers that get set to some value and then left at that value; parameters allow the set of equations to describe a whole family of dynamical systems.
are parameters in the system, numbers that get set to some value and then left at that value; parameters allow the set of equations to describe a whole family of dynamical systems.
What happened next (in the dramatic flow of time) is a story that’s been told over and over. Here’s how the American Physical Society tells it:
He [Lorenz] kept a continuous simulation running on an extremely primitive computer [!], which would produce a day’s worth of virtual weather every minute. The system was quite successful at producing data that resembled naturally occurring weather patterns: nothing ever happened the same way twice, but there was clearly an underlying order.
One day in the winter of 1961, Lorenz wanted to examine one particular sequence at greater length, but he took a shortcut. Instead of starting the whole run over, he started midway through, typing the numbers straight from the earlier printout to give the machine its initial conditions. Then he walked down the hall for a cup of coffee, and when he returned an hour later, he found an unexpected result. Instead of exactly duplicating the earlier run, the new printout showed the virtual weather diverging so rapidly from the previous pattern that, within just a few virtual “months”, all resemblance between the two had disappeared.
At first Lorenz assumed that a vacuum tube had gone bad in his computer, a Royal McBee, which was extremely slow and crude by today’s standards. Much to his surprise, there had been no malfunction. The problem lay in the numbers he had typed. Six decimal places were stored in the computer’s memory: .506127. To save space on the printout, only three appeared: .506. Lorenz had entered the shorter, rounded-off numbers assuming that the difference [of] one part in a thousand was inconsequential.
["This Month in Physics History: 'Circa January 1961: Lorenz and the Butterfly Effect' ", APS News, January 2003.]
This was a shocking result. The system of equations he was studying was nonlinear, and it is well-known that nonlinear systems can amplify small differences — Lorenz did not discover nonlinear amplification as some have written. But this divergence of the solutions was extreme: after not much time the two solutions not only weren’t close, they were so far apart that it looked like they never had anything to do with each other. This is a characteristic known as extreme sensitivity to initial conditions.
What’s more, one could put in virtually identical initial conditions all day long and keep getting different results a little ways down the road. In fact, the state of the system at these later times was unpredictable in practical terms — the system was chaotic in behavior.
That chaotic behavior was shocking result number two. Chaotic behavior had long been associated with nonlinear systems, but not with such simple systems. The behavior seemed, in essence, random, but there is no randomness at all in the equations: they are fully deterministic.** Thus, this characteristic later became known as deterministic chaos.
Lorenz looked at the behavior of the solutions by drawing graphs of pairs of the dynamical variables as time progressed. The resulting paths are known as the system’s trajectory in phase space. The trajectory for his set of equations looped around on two different spirals, never settling down to a single line and shifting sides from one spiral to the other at unpredictable intervals. (See this image for a beautiful example that illustrates these ideas.) The image above shows how the trajectory looks, seen in quasi-3D. (Follow the strings of dots as they swoop about one loop and then fly to the other side.)
These phase-space trajectories where unlike anything seen before. Usually a trajectory would settle down into an orbit that, after some time had passed, would never change, or maybe the orbit would decay and just settle into a point where it would stay forever. Think of a coin rolling around on its side on the floor: after awhile the coin flops over and just sits on the floor in one spot forever after.
There was another oddity, too, in these phase-space trajectories Lorenz plotted. Dynamical systems that are deterministic have trajectories in phase space that never cross themselves–it’s just the way the mathematics works. However, Lorenz’ trajectories did appear to cross themselves and yet, to speak loosely, they never got tangled up. The best he could say at the time was that the planes that the trajectories were in seemed, somehow, like an infinitely thin stack of planes that kept the trajectories apart, or something.
He published his results in the March, 1963 issue of the Journal of the Atmospheric Sciences; you can download the paper online from this page, which has the abstract of the paper on it. If you look at the paper you might see that Lorenz simply didn’t have the vocabulary at the time to talk about the behavior of this system. All of that was developed about a decade later. Very few people saw his original paper and it had little impact until it was rediscovered c. 1970.
These points or orbits in phase space that are the long-time trajectories of dynamical systems are known as the attractors in the phase space, for rather obvious reasons. The Lorenz Attractor, as it became know, was an altogether stranger fish than those normal attractors. As part of the rediscovery of Lorenz’ work, in a famous and highly unreadable paper by David Ruelle and Floris Takens (“On the nature of turbulence”, Communications of Mathematical Physics 20: 167-192; 1971) the term strange attractor was created to describe such dynamical oddities of deterministic chaos as the Lorenz Attractor.##
Strange attractors have had quite the vogue, as has deterministic chaos in dynamical systems. The characteristic feature of deterministic chaos, in addition to its unpredictability, is its extreme sensitivity to initial conditions.&& Also in the seventies Benoit Mandelbrot’s work on fractals began to enter the mathematical-physics consciousness and the concepts developed that allowed strange attractors to be described as having non-integer dimensions in phase space. The dimension of the Lorenz Attractor is about 2.06, so it’s almost but not quite flat or, alternatively, it’s the “thick” plane that Lorenz originally conceptualized.
Lorenz has contributed to the popular culture, but few people are aware of it. His original interest was in modeling the atmosphere in the context of weather forecasting. His discovery of the Lorenz attractor and deterministic chaos (albeit not called that at the time) made it suddenly apparent that there were probably limits to how long the “long” in “long-term forecasting” could be. As he put it in the abstract to his paper, “The feasibility of very-long-range weather prediction is examined in the light of these results.” Very understated! There’s no direct calculation of the time involved–it’s probably impossible, or nearly so–but it’s generally thought that good forecasts don’t go much beyond three days. Check your own five-day forecasts for accuracy and you’ll start to see just how often things go awry around day five. The point here is that weather models are very good but there are fundamental limitations on forecasting because of the system’s extreme sensitivity to initial conditions.††
If you’ve been reading the footnotes, you already know that Lorenz gave a paper at a AAAS meeting in 1972 titled “Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas?” And that’s how the extreme sensitivity to initial conditions of systems exhibiting deterministic chaos became known as “the butterfly effect”.
For pretty good reasons, many people are fascinated by creating images of the Lorenz Attractor. Among other reasons it seems infinitely variable and, well, so strange. This Google images search for “Lorenz attractor” can get you started on that exploration.
———-
† This is my source page for the image, which itself has an interesting history. It was rendered by Paul Bourke, who has a gallery featuring many beautiful images of fractals and strange attractors and related objects, of which this is just one example.
* Some obituaries:
Finally, Bob Park had this to say:
EDWARD N. LORENZ: THE FATHER OF CHAOS THEORY.
A meteorologist, Lorenz died Wednesday at 90. He found that seemingly insignificant differences in initial conditions can lead to wildly divergent outcomes of complex systems far down the road. At a AAAS meeting in 1972, the title of his talk asked “Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas.” Alas, the frequency of storms cannot be reduced by killing butterflies.
[Robert L. Park, What's New, 18 April 2008.]
‡ The equation set is derived from the full set of equations that describe Rayleigh-Bénard convection, which is thermally driven convection in a layer of fluid heated from below. In my early graduate-school days I did some research on the topic, which may explain my early interest in chaos and related topics.
# A “space” is quite a general thing and could be made up of any n variables and thereby be an “n-space”. However, the phrase “phase space” is generally reserved for n-spaces in which the n variables are specifically the variables found in the dynamical equations that define the dynamical system of interest. For present purposes, this footnote is entirely optional.
** Deterministic here means pretty much what one thinks it would mean, but more specifically it means being single-valued in the time variable, or, equivalently, that the solutions of the equations reverse themselves if time is run backwards. Virtually all real dynamical systems are invariant under time reversal.
## I tried to read part of the paper once. I remember two things about it. One was that they said the paper was divided into two sections, the first more popular in development, the second more mathematical; I couldn’t get past the first page of the first section. But I also remember how they developed some characteristics of these attractors, which seemed very peculiar at the time, and then they simply said: “We shall call such attractors ‘strange’.” Et voilà!
&& Also expressed as exponential divergence of phase-space trajectories.
†† The Met–the UK Meteorological Office–has an interesting series of pages about how weather forecasting works in practice, starting at “Ensemble Prediction“. The Lorenz attractor appears on the second page of that series, called “The Concept of Ensemble“.
Feb
24
Posted by jns on
February 24, 2008
 This week’s beard belongs to Albrecht Dürer, easily in my top-10 of most extraordinary artists ever. This amazing self-portrait was painted when the artist was 29 years old, in the year 1500. Is it symbolic that Dürer paints himself in this remarkably self-possessed, self-confident pose, looking directly at the viewer? It’s also interesting that he paints himself more as an aristocrat rather than with the commonly affected palette in hand, as a painter. What is the power in this painting that makes it feel so much as though it communicates directly with the viewer across the more than five centuries since Dürer painted it. Honestly, it creates for me a frisson that very few works of art manage to do.
This week’s beard belongs to Albrecht Dürer, easily in my top-10 of most extraordinary artists ever. This amazing self-portrait was painted when the artist was 29 years old, in the year 1500. Is it symbolic that Dürer paints himself in this remarkably self-possessed, self-confident pose, looking directly at the viewer? It’s also interesting that he paints himself more as an aristocrat rather than with the commonly affected palette in hand, as a painter. What is the power in this painting that makes it feel so much as though it communicates directly with the viewer across the more than five centuries since Dürer painted it. Honestly, it creates for me a frisson that very few works of art manage to do.
Dürer was born in Nuremberg, Germany in 1471 (21 May), and he died in Nuremberg, Germany in 1528 (6 April). He did not stay his entire life in Nuremberg, but it seems that it was his center and he returned there after his various excursions to Italy and the Netherlands. He was a master of drawing, painting, printmaking, and engraving. He helped develop the newly emerging technique of perspective. He died relatively wealthy, apparently making his money from his prints, for which he was justly celebrated across Europe. (The Wikipedia biography of Dürer is nicely done; I also enjoyed the biography and the lovely images of stamps featuring works by Dürer on this page from Art History on Stamps.)
This page from WebMuseum, Paris has a nice collection of images, some biography, and a useful discussion of his portraiture. I don’t see much point in trying to name any particular favorites, although this self-portrait I certainly put on his list of masterworks. Also famous, and for good reason, are his smallish, early watercolors “A Young Hare” and “The Large Turf“. Both are breathtaking in their amazing realism, yet they go beyond mere realism and seem to breathe with a vitality beyond what any photograph could conjure for these subjects.
When we were in Rome in 2001, we happened upon a small exhibit concerning prints and printmaking through history, and there we saw some Dürer first hand. There was a copy of his notorious print of a Rhinoceros (notorious for being notably inaccurate, apparently drawn from a verbal description of the first rhino to arrive in Europe). We also saw two amazing “oversized” woodcuts (describing them as “oversized” seems such an understatement!) “The Triumphal Arch and the Large Triumphal Carriage of Maximilian I”, which are discussed at some length, along with some remarkable photographs of the works, on this page.
Seeing these things first hand was quite an experience that still feels very close to me.
Nov
21
Posted by jns on
November 21, 2007
From this week’s Physics News Update* a note about physicist Luis Alvarez, to whom all things were interesting. In case you’ve ever wondered about the source of the hypothesis that the dinosaurs were wiped out by a meteorite, read on.
EGYPTIAN PYRAMIDS, DINOSAUR EXTINCTION, THE JFK ASSASSINATION: all were studied by Berkeley physicist Luis Alvarez. Alvarez won a Nobel Prize for his discovery of new particles using a bubble chamber, but some of his fame comes from his work applying physics principles and methods outside the normal physics-research world. In the November issue of the American Journal of Physics, Charles Wohl of the Lawrence Berkeley National Lab looks at three notable examples of Alvarez*s extracurricular effort.
(1) To search for possible hidden chambers in the Chephren pyramid in Cairo-one of the three great pyramids built in the third millennium BCE-Alvarez designed an experiment in which cosmic rays would strike a detector set up inside a known chamber beneath the pyramid. Observing the penetrating muons from cosmic-ray showers, this detector would discern any intervening empty spaces in the overlying pyramid structure. The upshot: no hidden chambers.
(2) In scrutinizing the so called “Zapruder film”, a short filmed sequence that caught the assassination in progress, experts had been puzzled by the backwards jerk of President Kennedy’s head after one of the bullet impacts. Some took this to be evidence for another assassin shooting from in front of the president’s car. Alvarez and some of his colleagues performed impromptu experiments at a shooting range, and also considered the conservation of momentum and the forward-moving matter from the wound. From this they concluded that the movie sequence was consistent with a shot coming from the rear.
(3) Most famous of all was Alvarez’s hypothesis, made in collaboration with his son Walter Alvarez, that a thin but conspicuous layer of the otherwise rare element iridium in numerous places around the world, all at a geological stratum corresponding to the era just around the boundary between the Cretaceous and Tertiary periods (the KT boundary), signified a large asteroid impact at that time. This impact, it was further thought, cast enough dust into the air from a long enough time as to kill off many living things, including a large portion of dinosaurs.
———-
* Phillip F. Schewe, Physics News Update, The American Institute of Physics Bulletin of Physics News, Number 847, 20 November 2007.
Dec
07
Posted by jns on
December 7, 2006
 This week’s beard is worn by none other than Charles Darwin (12 February 1809 – 19 April 1882), the infamous, the reviled, the namesake of the dreaded Darwinism, author of On the Origin of Species by Means of Natural Selection.
This week’s beard is worn by none other than Charles Darwin (12 February 1809 – 19 April 1882), the infamous, the reviled, the namesake of the dreaded Darwinism, author of On the Origin of Species by Means of Natural Selection.
Quite without my really meaning for it to happen, the past month or more has been my Darwin month: I’ve been reading books with Darwin and Darwinism (or, perhaps more precisely, “post-synthesis neo-Darwinism”) as their themes, and it’s been a rewarding period of Darwinian immersion. The books in question are The Blind Watchmaker, by Richard Dawkins, Darwin’s Dangerous Idea, by Daniel Dennett, and “The Reluctant Mr. Darwin”, by David Quammen. The Dawkins is the only one I’ve finished so far — the others are in progress. Sometime after they’re all finished I expect I’ll write some Book Notes about them.
The Dawkins and the Dennett book both have very similar goals, namely, to elucidate the central idea of Darwinism* at some length to reduce the mystery, misunderstanding, and hostility that it engenders. They both do a good job in markedly different voices: Dawkins is a high-energy, exuberant acolyte, Dennett a more deliberate and philosophical adherent. Quammen’s book, it seems, intends to be an intellectual biography of how Darwin came to his theory about evolution and what happened when he finally arrived there; I’m still near the beginning but it promises to be a good trip.
In his introduction, Quammen touches on those famous polls by Gallup and the Pew Research Center that keeps finding that some 45% of the American people believe that “God created human beings pretty much in their present form at one time within the last 10,000 years or so”; only 13% agreed that humans have developed from other life forms without any intervention from God! He writes:
Maybe the polls are invalid. Maybe the numbers would be much different in England or Sweden or India. Maybe the same distinctly American mixture of skepticism and evangelicalism that led to the Scopes trial, in 1925, continues to animate many citizens who would simply rather take their biology from scripture than from science. Maybe the question of human evolution is misleading and inordinately touchy; maybe Gallup and Pew should be asking whether God created, let’s say, tree kangaroos in their present form. Or maybe … who knows? I don’t claim to have any definitive explanation for such an extreme level of skepticism and willful antipathy toward such a well-established scientific discovery. Frankly, it mystifies me. But certainly those Gallup results–combined with the continuing political offensive against teaching evolutionary biology in public schools–testify that Charles Darwin isn’t just perennially significant. He’s also urgently relevant to education and governance.
I have agree with Quammen when he says “Frankly, it mystifies me.” Although I didn’t do it because of Darwinism as such, or to fight specifically against creationist incursions, this mystification is certainly part of the reason I founded Ars Hermeneutica, Limited. Now, whether we’ll be able to understand or do anything about the problem is an entirely different animal, but we intend to try.
———-
*That species are not persistent and unchanging, but that species evolve from other species through the agency of natural selection.
Sep
12
Posted by jns on
September 12, 2006
Isaac and I have both recently finished reading Tycho & Kepler, by Kitty Ferguson, and we thoroughly enjoyed it. (There’s more about the book in our Science Besieged Book Note.) Thus it happens that this beard and rather extravagent mustache belongs to the Danish astronomer Tycho Brahe.
Tycho, active in the second half of the 16th century, is often described as the greatest naked-eye astronomer in history. The biggest reason for this is that the telescope was just being invented — it was only in 1610 that Galileo discovered the moons of Jupiter in one of the earliest astronomical uses of the telescope. Think for a moment of what it must have been like to try to do science when, as Ms. Ferguson pointed out, geometry was the most advanced mathematics known. Calculus would not be invented by Newton & Leibnitz for nearly another century.
Regardless, he created some magnificent and clever instruments with which he made observations of unprecedented precision. In particular, he measured the orbits of the planets with enough accuracy that, just after Tycho’s death, Kepler finally hit on his (Kepler’s) 3 Laws of Planetary Motion and announced that the planets followed eliptical orbits. (The eccentricity of the orbits, which is to say the amount by which they are elliptical rather than circular, was very small and barely discernable.)
These portraits of Tycho do not represent his reddish-blond beard and quite remarkable mustache too clearly, but Ms. Ferguson’s description makes it clear that he was physically rather to my taste:
Tycho had just turned twenty-nine [in 1575] and was an experienced courtier, polished by his travels and attendance at many courts. Garbed appropirately with flowing cape, feathered hat, and sword, he was an imposing figure, barrel-chested, elegant, and of distinctly noble bearing. His eyes were light-colored, and his hair, beard, and substantial mustache were reddish blond. In portraits, his false nose looks a fairly successful imitation, close to flesh-colored — though an astute portrait painter would have made it so in any case. [p. 72]
[from: Kitty Ferguson, Tycho & Kepler : The Unlikely Partnership That Forever Changed Our Understanding of the Heavens. New York : Walker & Company, 2002.]
Oh, about the nose: in his youth Tycho got a substantial portion of his nose cut off during a rather pointless duel. Although it is true that he had an ersatz nose fashioned of gold alloy, it was for special occasions only. For everyday use he had a copper and tin alloyed nose. He had made both noses himself.


 This is chemist Richard Willstätter. I confess that his name was not familiar to me despite his having won the 1915 Nobel Prize in chemistry.
This is chemist Richard Willstätter. I confess that his name was not familiar to me despite his having won the 1915 Nobel Prize in chemistry. The image at right is a gorgeous rendering† of a mystifying object known as the Lorenz Attractor. It shares its name with Edward Lorenz, its discoverer, who died earlier this month at the age of 90.* Edward Lorenz is sometimes called “the father of chaos”, and the Lorenz attractor is the reason.
The image at right is a gorgeous rendering† of a mystifying object known as the Lorenz Attractor. It shares its name with Edward Lorenz, its discoverer, who died earlier this month at the age of 90.* Edward Lorenz is sometimes called “the father of chaos”, and the Lorenz attractor is the reason. 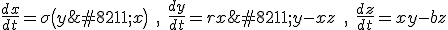
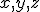 , by the way, are not spatial variables but instead more abstract variables that represent wind velocity, pressure, and temperature in the atmosphere. You can still think of them, though, as the three dimensions of an abstract “space” that is referred to as “phase space”.# The
, by the way, are not spatial variables but instead more abstract variables that represent wind velocity, pressure, and temperature in the atmosphere. You can still think of them, though, as the three dimensions of an abstract “space” that is referred to as “phase space”.# The 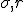 and
and 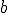 are parameters in the system, numbers that get set to some value and then left at that value; parameters allow the set of equations to describe a whole family of dynamical systems.
are parameters in the system, numbers that get set to some value and then left at that value; parameters allow the set of equations to describe a whole family of dynamical systems.  This week’s beard belongs to Albrecht Dürer, easily in my top-10 of most extraordinary artists ever. This amazing self-portrait was painted when the artist was 29 years old, in the year 1500. Is it symbolic that Dürer paints himself in this remarkably self-possessed, self-confident pose, looking directly at the viewer? It’s also interesting that he paints himself more as an aristocrat rather than with the commonly affected palette in hand, as a painter. What is the power in this painting that makes it feel so much as though it communicates directly with the viewer across the more than five centuries since Dürer painted it. Honestly, it creates for me a frisson that very few works of art manage to do.
This week’s beard belongs to Albrecht Dürer, easily in my top-10 of most extraordinary artists ever. This amazing self-portrait was painted when the artist was 29 years old, in the year 1500. Is it symbolic that Dürer paints himself in this remarkably self-possessed, self-confident pose, looking directly at the viewer? It’s also interesting that he paints himself more as an aristocrat rather than with the commonly affected palette in hand, as a painter. What is the power in this painting that makes it feel so much as though it communicates directly with the viewer across the more than five centuries since Dürer painted it. Honestly, it creates for me a frisson that very few works of art manage to do. This week’s beard is worn by none other than Charles Darwin (12 February 1809 – 19 April 1882), the infamous, the reviled, the namesake of the dreaded Darwinism, author of On the Origin of Species by Means of Natural Selection.
This week’s beard is worn by none other than Charles Darwin (12 February 1809 – 19 April 1882), the infamous, the reviled, the namesake of the dreaded Darwinism, author of On the Origin of Species by Means of Natural Selection.
