GRB 090423

This luminous blob is a “gamma-ray burster”, and exceedingly distant from us: slightly over 13 billion light-years. In fact, it is the current record-holder in the “most distant object seen” category. It was spotted recently by NASA’s Swift spacecraft (about the spacecraft; and about the Swift mission).

Just how a gamma-ray burst happens is still being studied — it’s a big reason behind the Swift mission. GRBs seem to be associated with star remnants collapsing into black holes following a supernova event.

Following the explosion of a big enough star (see “A Star Explodes in Slow Motion“), a shell of matter is expanding around a core that is collapsing into the singularity known as a black hole. In all likelihood this collapsing matter is rotating at very high velocity.

It is thought that lumps of matter falling into the black hole cause some matter to be ejected at very high velocity away from the center in a narrowly collimated jet at relativistic speeds. As this jet passes through the expanding shell of matter around the object, interactions between the jet and the shell of matter produce radiation across a wide spectrum but still in a narrowly visible cone. Sometimes we are fortunate that one of those cones is headed in our direction.

Of this event the NASA press release (“New Gamma-Ray Burst Smashes Cosmic Distance Record“; also source of the image above) says

April 28, 2009: NASA’s Swift satellite and an international team of astronomers have found a gamma-ray burst from a star that died when the universe was only 630 million years old–less than five percent of its present age. The event, dubbed GRB 090423, is the most distant cosmic explosion ever seen. [...]

The burst occurred at 3:55 a.m. EDT on April 23rd. Swift quickly pinpointed the explosion, allowing telescopes on Earth to target the burst before its afterglow faded away. Astronomers working in Chile and the Canary Islands independently measured the explosion’s redshift. It was 8.2, smashing the previous record of 6.7 set by an explosion in September 2008. A redshift of 8.2 corresponds to a distance of 13.035 billion light years.

“We’re seeing the demise of a star — and probably the birth of a black hole — in one of the universe’s earliest stellar generations,” says Derek Fox at Pennsylvania State University [where the flight operations staff is located].

That is incredibly far away!

Equality Advances, Pie Charts Decline

Via Joe.My.God I learn that a new CBS News / New York Times poll shows an amazing 42% of those polled in favor of legal marriage for same-sex couples. That’s amazing because the previous poll by the same group only one month ago found only 33% in favor of legal marriage. This increase of 9 points lies well outside the sampling error of the poll and must represent some significant fall-out from the addition of Iowa and Vermont to the growing list of states with marriage equality.

That’s interesting enough, but this graphic from CBS (source for graphic and poll results) is also interesting:

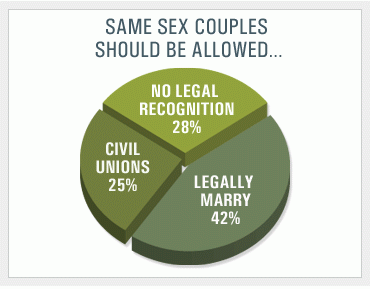
One thing to note is that fully two-thirds of those polled support some sort of legal recognition for same-sex couples.

The other thing to note is that there is a 5% wedge missing from the pie chart. Add up the percentages and you get 95%. Now, while it is not at all unusual to have some 5% of those asked who are undecided or who wish to give no opinion, it is not kosher to leave them out of the pie chart and sort of fudge the other wedges around to fill in the space.

Does this chart make it clear that there is a 5% wedge unaccounted for? Not at all. Somehow the wedges are made to look as though they fill 100% of the circle and yet they should not. You might think that 5% is small and wouldn’t be visible, but it amounts to one-fifth of the “civil unions” wedge, an amount that would be quite noticeable. So, the chart is inaccurate and misleading. I wonder which wedge, or wedges, got the undecideds?

Shame on CBS. I hate it when big corporations who could have science and math consultants without even noticing the cost can’t be bothered.
—–
[Updated a few minutes later:] In thinking about the poll results and the remarkable shift since the previous poll, Timothy Kincaid at Box Turtle Bulletin (“Americans Shift Sharply in Favor of Marriage“) gives a long list of significant steps that have been taken towards marriage equality in the interval between the polls.

Endangered Species Act Less Endangered

More signs today of a return to policy supported by science rather than science perverted to the will of policy.

Secretary of Commerce Gary Locke and Secretary of the Interior Ken Salazar today announced that the two departments are revoking an eleventh-hour Bush administration rule that undermined Endangered Species Act (ESA) protections. Their decision requires federal agencies to once again consult with federal wildlife experts at the U.S. Fish and Wildlife Service and the National Oceanic and Atmospheric Administration – the two agencies that administer the ESA – before taking any action that may affect threatened or endangered species.

“By rolling back this 11th hour regulation, we are ensuring that threatened and endangered species continue to receive the full protection of the law,” Salazar said. “Because science must serve as the foundation for decisions we make, federal agencies proposing to take actions that might affect threatened and endangered species will once again have to consult with biologists at the two departments.”

["Salazar and Locke Restore Scientific Consultations under the Endangered Species Act to Protect Species and their Habitats", NOAA Press Release, 28 April 2009.]

Our Spotless Sun

Last week (on 4 April 2009, to be precise), this item came from SpaceWeather.com:

SPOTLESS SUNS: Yesterday, NASA announced that the sun has plunged into the deepest solar minimum in nearly a century. Sunspots have all but vanished and consequently the sun has become very quiet. In 2008, the sun had no spots 73% of the time, a 95-year low. In 2009, sunspots are even more scarce, with the “spotless rate” jumping to 87%. We are currently experiencing a stretch of 25 continuous days uninterrupted by sunspots–and there’s no end in sight.

This is a big event, but it is not unprecedented. Similarly deep solar minima were common in the late-19th and early-20th centuries, and each time the sun recovered with a fairly robust solar maximum. That’s probably what will happen in the present case, although no one can say for sure. This is the first deep solar minimum of the Space Age, and the first one we have been able to observe using modern technology. Is it like others of the past? Or does this solar minimum have its own unique characteristics that we will discover for the first time as the cycle unfolds? These questions are at the cutting edge of solar physics.

There was a notable period of near sun-spotless activity between 1645 and 1715 known as the Maunder Minimum. There is a description in my posting “On Reading The Little Ice Age“.

The Maunder Minimum more or less coincided with one long cooling period in Europe, making it a darling of climate-change deniers who naively want to blame every climate shift on changes in solar activity.

What dire warnings will accompany the realization of the current solar minimum? Will the threatened climate disasters rival those due to god’s wrath over gay marriage? Only time will tell.

Two Benfords

This is physicist and science-fiction author Gregory Benford. His official website, source of the photograph, tells us that

Benford [born in Mobile, Alabama, on January 30, 1941] is a professor of physics at the University of California, Irvine, where he has been a faculty member since 1971. Benford conducts research in plasma turbulence theory and experiment, and in astrophysics.

Around 1990, the last time I was on a sci-fi binge, I read a number of his books; I see from the official list of novels that I’m behind by a number of books. I should pick up where I left off. I remember Benford’s writing as being very satisfactory from both a science viewpoint and from a fiction viewpoint, although I find that, in my mind, I confuse some of the story-memory details with plots by the late physicist and sci-fi author Charles Sheffield, to whom I give the edge in my preference for hard-science-fiction and adventuresome plots.

But, as is not unprecedented in this forum, Mr. Benford is really providing a pretext–a worthwhile pretext on several counts, clearly, but a pretext nonetheless, because I wanted to talk about “Benford’s Law” and that Benford did not wear a beard.

Frank Benford (1883-1948) was a physicist, or perhaps an electrical engineer–or perhaps both; sources differ but the distinctions weren’t so great in those days. His name is attached to Benford’s Law not because he was the first to notice the peculiar mathematical phenomenon but because he was better at drawing attention to it.

I like this quick summary of the history (Kevin Maney, “Baffled by math? Wait ’til I tell you about Benford’s Law“, USAToday, c. 2000)

The first inkling of this was discovered in 1881 by astronomer Simon Newcomb. He’d been looking up numbers in an old book of logarithms and noticed that the pages that began with one and two were far more tattered than the pages for eight and nine. He published an article, but because he couldn’t prove or explain his observation, it was considered a mathematical fluke. In 1963, Frank Benford, a physicist at General Electric, ran across the same phenomenon, tried it out on 20,229 different sets of data (baseball statistics, numbers in newspaper stories and so on) and found it always worked.

It’s not a terribly difficult idea, but it’s a little difficult to pin down exactly what Benford’s Law applies to. Let’s start with this tidy description (from Malcolm W. Browne, “Following Benford’s Law, or Looking Out for No. 1“, New York Times, 4 August 1998):

Intuitively, most people assume that in a string of numbers sampled randomly from some body of data, the first non-zero digit could be any number from 1 through 9. All nine numbers would be regarded as equally probable.

But, as Dr. Benford discovered, in a huge assortment of number sequences — random samples from a day’s stock quotations, a tournament’s tennis scores, the numbers on the front page of The New York Times, the populations of towns, electricity bills in the Solomon Islands, the molecular weights of compounds the half-lives of radioactive atoms and much more — this is not so.

Given a string of at least four numbers sampled from one or more of these sets of data, the chance that the first digit will be 1 is not one in nine, as many people would imagine; according to Benford’s Law, it is 30.1 percent, or nearly one in three. The chance that the first number in the string will be 2 is only 17.6 percent, and the probabilities that successive numbers will be the first digit decline smoothly up to 9, which has only a 4.6 percent chance.

Take a long series of numbers drawn from certain broad sets, and look at the first digit of each number. The frequency of occurrence of the numerals 1 through 9 are not uniform, but distributed according to Benford’s Law. Look at this figure that accompanies the Times article:

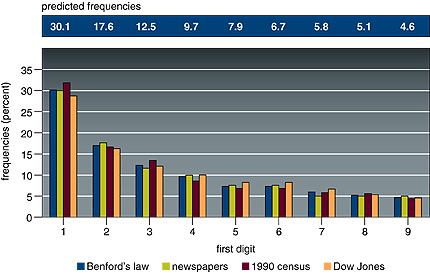
Here is the original caption:

(From “The First-Digit Phenomenon” by T. P. Hill, American Scientist, July-August 1998)

Benford’s law predicts a decreasing frequency of first digits, from 1 through 9. Every entry in data sets developed by Benford for numbers appearing on the front pages of newspapers, by Mark Nigrini of 3,141 county populations in the 1990 U.S. Census and by Eduardo Ley of the Dow Jones Industrial Average from 1990-93 follows Benford’s law within 2 percent.

Notice particularly the sets of numbers that were examined for the graph above: numbers from newspapers (not sports scores or anything sensible, just all the numbers from their front pages), census data, Dow Jones averages. These collections of numbers do have some common characteristics but it’s a little hard to pin down with precision and clarity.

Wolfram Math (which shows a lovely version of Benford’s original example data set halfway down this page) says that “Benford’s law applies to data that are not dimensionless, so the numerical values of the data depend on the units”, which seems broadly true but, curiously, is not true of the original example of logarithm tables. (But they may be the fortuitous exception, having to do with their logarithmic nature.)

Wikipedia finds that a sensible explanation can be tied to the idea of broad distributions of numbers, a distribution that covers orders of magnitude so that logarithmic comparisons come into play. Plausible but not terribly quantitative.

This explanation (James Fallows, “Why didn’t I know this before? (Math dept: Benford’s law)“, The Atlantic, 21 November 2008) serves almost as well as any without going into technical details:

It turns out that if you list the population of cities, the length of rivers, the area of states or counties, the sales figures for stores, the items on your credit card statement, the figures you find in an issue of the Atlantic, the voting results from local precincts, etc, nearly one third of all the numbers will start with 1, and nearly half will start with either 1 or 2. (To be specific, 30% will start with 1, and 18% with 2.) Not even one twentieth of the numbers will begin with 9.

This doesn’t apply to numbers that are chosen to fit a specific range — sales prices, for instance, which might be $49.99 or $99.95 — nor numbers specifically designed to be random in their origin, like winning lottery or Powerball figures or computer-generated random sums. But it applies to so many other sets of data that it turns out to be a useful test for whether reported data is legitimate or faked.

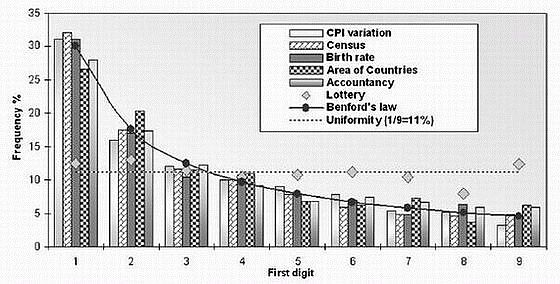
Here’s yet another graph of first digits from vastly differing sets numbers following Benford’s Law (from Lisa Zyga, “Numbers follow a surprising law of digits, and scientists can’t explain why“, physorg.com, 10 May 2007); again one should note the extreme heterogeneity of the number sets (they give “lottery” results to show that, as one truly wants, the digits are actually random):

The T.P. Hill mentioned above (in the caption to the first figure), is a professor of mathematics at Georgia Tech who’s been able to prove some rigorous results about Benford’s Law. From that institution, this profile of Hill (with an entertaining photograph of the mathematician and some students) gives some useful information:

Many mathematicians had tackled Benford’s Law over the years, but a solid probability proof remained elusive. In 1961, Rutgers University Professor Roger Pinkham observed that the law is scale-invariant – it doesn’t matter if stock market prices are changed from dollars to pesos, the distribution pattern of significant digits remains the same.

In 1994, Hill discovered Benford’s Law is also independent of base – the law holds true for base 2 or base 7. Yet scale- and base-invariance still didn’t explain why the rule manifested itself in real life. Hill went back to the drawing board. After poring through Benford’s research again, it clicked: The mixture of data was the key. Random samples from randomly selected different distributions will always converge to Benford’s Law. For example, stock prices may seem to be a single distribution, but their value actually stems from many measurements – CEO salaries, the cost of raw materials and labor, even advertising campaigns – so they follow Benford’s Law in the long run. [My bold]

So the key seems to be lots of random samples from several different distributions that are also randomly selected: randomly selected samples from randomly selected populations. Whew, lots of randomness and stuff. Also included is the idea of “scale invariance”: Benford’s Law shows up in certain cases regardless of the units used to measure a property–that’s the “scale” invariance–which implies certain mathematical properties that lead to this behavior with the logarithmic taste to it.

Another interesting aspect of Benford’s Law is that it has found some applications in detecting fraud, particularly financial fraud. Some interesting cases are recounted in this surprisingly (for me) interesting article: Mark J. Nigrini, “I’ve Got Your Number“, Journal of Accountancy, May 1999. The use of Benford’s Law in uncovering accounting fraud has evidently penetrated deeply enough into the consciousness for us to be told: “Bernie vs Benford’s Law: Madoff Wasn’t That Dumb” (Infectious Greed, by Paul Kedrosky).

And just to demonstrate that mathematical fun can be found most anywhere, here is Mike Solomon (his blog) with some entertainment: “Demonstrating Benford’s Law with Google“.