Accepting PI

Posted by jns on November 24, 2008

This is Euclid (c. 365 BCE — c. 275 BCE) of Alexandria, Egypt, possibly one of the earliest celebrities to use only one name. Euclid is famous, of course, for writing Elements, his 13-book exposition on geometry and the earliest mathematical textbook and second only to the Bible in the number of editions published through history.

Invoking Euclid’s name is a ruse. Although there are any number of things related to Euclid and the Elements that we could discuss, what I’ve really been thinking about lately is , and I needed a pretext. In fact, it wasn’t even exactly that I’ve been thinking about so much as people’s relationship with the idea of .

It’s a trivial thing in a way, but I was perplexed to discover that some googler had reached a small article I had written (“Legislating the Value of Pi“, about the only actual case in history of an attempt to do so–in Indiana) by searching for “accepted value of pi”.

That disturbed me, although I’m finding it difficult to explain why. Let’s talk for a moment about the difference between physical constants and mathematical constants.

In physical theory there are any number of “physical constants”, numbers (with no units) or quantities (with units) that show up in physical theories and are generally presumed to be the same everywhere in the universe and often described as “fundamental” because they can’t be reduced to other other known values. Examples that might be familiar: “c”, the speed of light in a vacuum; “G”, Newton’s universal constant of gravitation; “e”, the charge of the electron; “”h”, Planck’s constant, ubiquitous in quantum mechanics; the list is lengthy. (You can find a long list and a bunch about physical constants at a page maintained by NIST the National Institute of Science and Technology.)

Fundamental physical constants are measured by experiment; that is the only way to establish their value. Some have been measured to extraordinary accuracy, as much as 12 decimal places (or to one part in one-million-million). The NIST website has an “Introduction to the constants for nonexperts“, which you might like to have a look at. (I never quite made it to being a fundamentals-constant experimentalist, but I did do high-precision measurement.)

Now, contrast the ontological status of fundamental constants with mathematical constants, things like ““, the ratio of the circumference to the diameter of a circle; “e”, the base of the natural logarithms; “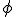“, the “golden ratio”, and numbers of that ilk. These are numbers that are perfectly well defined by known and exact mathematical relationships. (I once discussed a number of mathematical equations involving “” in “A Big Piece of Pi“.)

Now, it may be something odd about the way my mind works (that would be no real surprise), but to me there is a difference in status between fundamental physical constants, which must be measured and will forever be subject to experimental limitations in determining their values, and mathematical constants, which can always be calculated to any desirable precision (number of digits) using exact mathematical expressions.

To me, one can reasonably ask about the “current accepted values” of fundamental physical constants–indeed, you’ll see a similar expression (“adopted values”) on the NIST page–but that “accepted value” makes no sense when used to describe mathematical constants that simply have not been calculated as yet to the precision one might desire. And so, asking about the “accepted value” of seems like an ill-formed question to me. Your mileage is almost certain to vary, of course.

Well, now that you’ve made it through that ontological patch of nettles, it’s time for some entertainment. In the aforementioned article I had already discussed some of the fascinating mathematical equations involving , so we’re just going to have to make do with something a little different, even though it is still an equation involving you know what.

The problem of “Buffon’s Needle” was first put forward in the 18th century by Georges-Louis Leclerc, Comte de Buffon. I like the way Wikipedia states it (or find another discussion here):

Suppose we have a floor made of parallel strips of wood, each the same width, and we drop a needle [whose length is the same as the width of the strips of wood] onto the floor. What is the probability that the needle will lie across a line between two strips?

Worked it out yet?

You can always measure an approximate value of the probability for yourself with a needle and a sheet of paper on which you have ruled parallel lines separated by the length of the needle. Drop the needle on the paper a whole bunch of times. Divide the number of times the needle lands on a line by the total number of times you dropped the needle. What value do you get closer to the more times you do the drop the needle?

The answer: 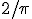. Exactly.