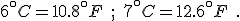Differences in Celsius & Fahrenheit

Posted by jns on March 31, 2008

Here’s an unexpected bit of innumeracy.

I’m about to finish up a book by Colin Tudge called The Time Before History : A Million Years of Human Impact (New York : Scribner, 1996; 366 pages). I expect there will be a book note soonish.

Anyway, here are two quotations from two nearby pages. See if you spot the problem.

We know, too, as related in chapter 2, that when the ice ages ended, they could, in any one place, end fast. Twenty years could see a 7°C (44°F) rise in temperature; the difference between a frozen landscape and a temperate one. [p. 301]

Besides, at the trough of the last ice age, 18,000 years ago, the surface of the sea in the eastern Mediterranean is known to have cooled by more than 6°C (43°F), which in ecological terms is huge, and yet the elephants and their miniaturized neighbors came through those harsh times. [p. 302]

Your reaction may be different, but the author’s–or editor’s!–error in converting the temperature differences from Celsius to Fahrenheit stands out to me as though written in flashing neon. Could they really believe that the temperature of the Mediterranean had changed by an amazing 43°F? “Huge” is one thing, but that’s huge!

Not so long ago I wrote at excessive length about how to convert values on one temperature scale to values on the other. What I didn’t talk about was how to compare temperature differences.

Look again at the formula for converting Celsius temperatures to Fahrenheit temperatures:

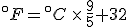
If we talk a bit about this equation, there are two things that it is telling us:

1. That Celsius degrees are bigger, nine-fifths bigger, than Fahrenheit degrees, which means that it takes fewer Celsius degrees to express a temperature change than Fahrenheit degrees; and
2. That the zero points on the two scales are offset by 32°F.

But this equation and this explanation refer to converting temperature values on one scale to the other. If we want to talk about temperature differences, that’s another matter, and that’s why it’s good to talk/think about what the equation above is saying.

Suppose we have two temperature values specified on the Celsius scale; call them 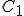and 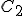. Then, to find the corresponding temperature difference expressed in terms of Fahrenheit degrees, we need to write down these two equations:

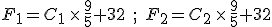
and then subtract one from the other. Do the algebra and you find

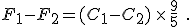
You’ll notice that the offset value of 32 disappears when you do the subtraction. This is as we expected because we had just talked about how Celsius degrees are nine-fifths bigger than Fahrenheit degrees.

But now you can see the error made by the author or his editor: they erroneously used the equation to convert temperatures on the Celsius scale to temperatures on the Fahrenheit scale, rather than merely change a temperature difference from degrees of one size to degrees of another size.

The innumeracy aspect is that, before using the conversion equation, one should know what it is saying. This simple step would alert anyone that 6°C could never be 43°F. Knowing that Celsius degrees are nine-fifths bigger than Fahrenheit degrees let’s us write the correct values for these temperature differences immediately: