When Celsius = Fahrenheit

Posted by jns on 6 February 2008

A while back, someone ended up at a page on this blog by asking Google for “the temperature at which the Celsius scale and Fahrenheit scale are the same number”. I don’t think they found the answer because I’d never actually discussed that question¹, but I thought the question was pretty interesting and discussing the answer might be a bit of good, clean rocket-science fun.

Actually, there is a prior question that I think is interesting, namely: how do we know that there is a temperature where the Celsius and Fahrenheit scales agree? The answer to that question is related to a simple mathematical idea.² We can picture this mathematical idea by drawing two lines on a chalkboard (or whiteboard) with a rule.

First, draw line A any way you want, but make it more horizontal than vertical, just to keep things clear. Now, draw line B in such a way that it’s point farthest left is below line A, but its point farthest right is above line A. What you will always find that that line B and line A will cross at some point. This may seem like an obvious conclusion but it is also a very powerful conclusion. Now, knowing where they will cross is another, often more difficult, question to answer.

How do we know, then, that the Fahrenheit and Celsius lines cross? Well, the freezing point of water, say, on the Celsius scale is 0°C, and on the Fahrenheit it is 32°F. On the other hand, absolute zero is -273.15°C, but -459.67°F. So, at the freezing point of water the Fahrenheit line is above the Celsius line, but at absolute zero that situation is reversed.

Finding the point where they cross is a simple question to answer with algebra. The equation that converts Fahrenheit degrees into Celsius degrees is

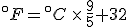
The equation that goes the other way is

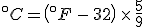
To find the temperature where the two lines cross, take one of the equations and set

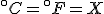
so that

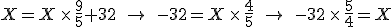
and then solve for 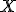. The result is that

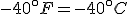
[Addendum: 19 February 2008, for the Kelvin & Fahrenheit folks]

The Kelvin scale of temperatures is a thermodynamic temperature scale: it’s zero point is the same as zero temperature in thermodynamic equations. It used Celsius-sized degrees, and there is indeed a temperature at which the Kelvin and Fahrenheit scales cross. The relation between the two is

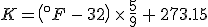
(Note that the absolute temperature scale uses “Kelvins” as the name of the units, and not “degrees Kelvin”.) As in the Fahrenheit / Celsius example, set 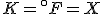and solve for 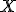, with the result that

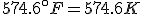
As before, Fahrenheit degrees are larger than Kelvins and will eventually overtake them, but the initial difference between the zero points is much larger, so the crossing point is at a much higher temperature.
———-
¹Because of the way links on blogs select different combinations of individual posts, by days, by months, by topics, etc., internet search engines often present the least likely links as solutions to unusual word combinations in search strings. I find this phenomenon endlessly fascinating.

²The mathematical idea is one that I’ve always thought was a “Fundamental Theorem of [some branch of mathematics]“, but I’ve forgotten which (if I ever knew) and haven’t been able to identify yet. This is probably another effect of encroaching old-age infirmity.
I imagine — possibly remember — the theorem saying something like:

For a continuous function defined on the interval , for , takes on all values between and .