Archive for February, 2008
Feb
29
Posted by jns on
February 29, 2008
Bob Park seems reinvigorated by all the science-silliness and some non-silliness going on that he reports in the latest (29 February) edition of “What’s New“. (Subscription information here.) Between feeling lazy and amused, I decided to include it all!
1. FENCES: SOMETHING THERE IS THAT DOESN’T LOVE A WALL.
Technology makes us arrogant. A 28-mile pilot project for a high-tech “virtual fence” south of Tucson, which cost $100M, is now acknowledged to be a failure. The history of the world is a story of fences that failed: the Great Wall of China, the Red Sea, the Berlin Wall, Robert McNamara’s electronic wall dividing Vietnam, followed by the horror of Agent Orange. Securing the 2,000 mile border was expected to cost $7.6B; the estimate will now go up. But desperate people will find a way in spite of obstacles. By contrast, the border with Canada remains unsecured. Why would Canadians want to come here? About 200,000 illegal immigrants enter from Mexico each year. For $7.6B we could pay them $38,000 each to stay in Mexico. We would all be better off.
2. EVOLUTION: THE GOOD NEWS IS FROM FLORIDA.
Last week WN reported the happy news that the Board of Education had approved science standards that call for teaching “the scientific theory of evolution.” As Harold Kroto, 1996 Nobel Prize and professor of chemistry at Florida State, put it, “The phrase ‘scientific theory’ gives us the leverage to differentiate between theories that are supported by evidence and those that aren’t.” It also pleased a conservative legislator who was happy it wasn’t called a “scientific fact.” Scientists should make it a point to distinguish between “scientific theory” and biblical revelation, which is “not even a theory.” It never ends; legislation is now being considered that would allow criticisms of evolution to be taught.
3. CREATIONISM: THE BAD NEWS IS FROM TEXAS.
A strong editorial in today’s issue of Nature warns that the Institute for Creation Research (ICR), which moved from San Diego to Dallas last year, has applied to the Texas Higher Education Coordinating Board for the right to grant online master’s degrees in science education. An advisory board has recommended acceptance. Founded by Henry Morris in 1972, the ICR regards the Bible as an inerrant source of scientific and historical fact. The Board had been expected to vote on the application in January, but requested additional information. The vote is now expected at the boards 24 April meeting. Steven Weinberg, Physics Nobel 1979, who five years ago defended the rights of Texas school children to learn the natural laws that govern our existence http://bobpark.physics.umd.edu/WN03/wn091903.html , has urged the board to deny accreditation to the Creation Research Institute. Every Texas scientist should do the same.
4. PEW FORUM: THE U.S. RELIGIOUS LANDSCAPE.
Based on interviews with more than 35,000 Americans age 18 and older, the Pew survey finds a changing landscape. More than a quarter of Americans have left the faith they were born in. Americans who are unaffiliated with any religion have seen the greatest growth in numbers as a result. Catholicism has experienced the greatest net losses. Is there any indication that Americans are becoming more rational? Perhaps. About a fourth of those who are unaffiliated describe themselves as atheist or agnostic.
Feb
27
Posted by jns on
February 27, 2008
After Copernicus published De Revolutionibus in 1543, acceptance of the idea that the Earth orbited the Sun was neither immediate nor universal. Some appealed to common sense:
No one in his senses, or imbued with the slightest knowledge of physics will ever think that the earth, heavy and unwieldy from its own weight and mass, staggers up and down around its own centre and that of the sun; for at the slightest jar of the earth, we would see cities and fortresses, towns and mountains thrown down.
– Jean Bodin (1529–1596), quoted in Peter Watson, Ideas, (New York : HarperCollins, 2005), p. 517
Isn’t it interesting how some common sense becomes uncommon.
Feb
24
Posted by jns on
February 24, 2008
 This week’s beard belongs to Albrecht Dürer, easily in my top-10 of most extraordinary artists ever. This amazing self-portrait was painted when the artist was 29 years old, in the year 1500. Is it symbolic that Dürer paints himself in this remarkably self-possessed, self-confident pose, looking directly at the viewer? It’s also interesting that he paints himself more as an aristocrat rather than with the commonly affected palette in hand, as a painter. What is the power in this painting that makes it feel so much as though it communicates directly with the viewer across the more than five centuries since Dürer painted it. Honestly, it creates for me a frisson that very few works of art manage to do.
This week’s beard belongs to Albrecht Dürer, easily in my top-10 of most extraordinary artists ever. This amazing self-portrait was painted when the artist was 29 years old, in the year 1500. Is it symbolic that Dürer paints himself in this remarkably self-possessed, self-confident pose, looking directly at the viewer? It’s also interesting that he paints himself more as an aristocrat rather than with the commonly affected palette in hand, as a painter. What is the power in this painting that makes it feel so much as though it communicates directly with the viewer across the more than five centuries since Dürer painted it. Honestly, it creates for me a frisson that very few works of art manage to do.
Dürer was born in Nuremberg, Germany in 1471 (21 May), and he died in Nuremberg, Germany in 1528 (6 April). He did not stay his entire life in Nuremberg, but it seems that it was his center and he returned there after his various excursions to Italy and the Netherlands. He was a master of drawing, painting, printmaking, and engraving. He helped develop the newly emerging technique of perspective. He died relatively wealthy, apparently making his money from his prints, for which he was justly celebrated across Europe. (The Wikipedia biography of Dürer is nicely done; I also enjoyed the biography and the lovely images of stamps featuring works by Dürer on this page from Art History on Stamps.)
This page from WebMuseum, Paris has a nice collection of images, some biography, and a useful discussion of his portraiture. I don’t see much point in trying to name any particular favorites, although this self-portrait I certainly put on his list of masterworks. Also famous, and for good reason, are his smallish, early watercolors “A Young Hare” and “The Large Turf“. Both are breathtaking in their amazing realism, yet they go beyond mere realism and seem to breathe with a vitality beyond what any photograph could conjure for these subjects.
When we were in Rome in 2001, we happened upon a small exhibit concerning prints and printmaking through history, and there we saw some Dürer first hand. There was a copy of his notorious print of a Rhinoceros (notorious for being notably inaccurate, apparently drawn from a verbal description of the first rhino to arrive in Europe). We also saw two amazing “oversized” woodcuts (describing them as “oversized” seems such an understatement!) “The Triumphal Arch and the Large Triumphal Carriage of Maximilian I”, which are discussed at some length, along with some remarkable photographs of the works, on this page.
Seeing these things first hand was quite an experience that still feels very close to me.
Feb
21
Posted by jns on
February 21, 2008

This remarkable image of the Earth rising over the lunar horizon is actually what it seems to be. It is a frame captured from an HDTV video taken on 7 November 2007 by the Japanese KAGUYA spacecraft, which is currently orbiting the Moon on a surveying mission. They tell us that the Earth is seen rising over a spot that is near the south pole of the Moon.
The KAGUYA Image Gallery, the source of this image (click on “HDTV”),* is a delight to look through; every click brings more remarkable sights and insights.
I first learned about the KAGUYA image from this Science@NASA feature for 20 February 2008: “Who’s Orbiting the Moon?“. It gives a nice run-down of all the missions from various countries that already have satellites orbiting the Moon, or will soon.
———-
* I have cropped the image and reduced it substantially so that it will fit in these narrow confines. Visit the website to find the incredibly large, incredibly high-resolution original image.
Feb
20
Posted by jns on
February 20, 2008
This is a blog posting about itself. According to the blog-software statistics, this is my one-thousandth posting [at my personal blog, the source for this essay] since the first one I posted on 18 October 2004.* To be honest, I’m a bit surprised that I’m still writing here regularly three-plus years later. Evidently it works for me somehow.
I’ve noticed that one-thousand is an accepted milestone at which one is to reflect, look back, and perhaps look forward. Well, you can look back as easily as I can, and I don’t see much reason to try predicting the future since we’re going to go through it together anyway. Therefore I thought this article should be about itself.
Or, rather, the topic is things that are about themselves. So called self-referential (SR) things.
I believe that my introduction to SR things, at least as an idea, came when I read Douglas Hofstadter’s remarkable book “Gödel, Escher, Bach: An Eternal Golden Braid”. The book was published in 1979; my book of books tells me that I finished reading it on 17 August 1986, but I expect that that date is the second time that I read the book. I can remember conversations I had about the book taking place about 1980–and I didn’t start keeping my book of books until 1982.
Broadly speaking, GEB was about intelligence–possible consciousness–as an emergent property of complex systems or, in other words, about how the human brain can think about itself. Hofstadter described the book as a “metaphorical fugue” on the subject, and that’s a pretty fair description for so few words. Most of his points are made through analogy, metaphor, and allegory, and the weaving together of several themes. All in all, he took a very indirect approach to a topic that is hard to approach directly, and I thought it worked magnificently. In a rare fit of immodesty, I also thought that I was one of his few readers who would likely understand and appreciate the musical, mathematical, and artistic approaches he took to his thesis, not to mention how each was reflected in the structure of the book itself–a necessary nod to SR, I’d say, for a book that includes SR. There were parts of it that I thought didn’t work so successfully as other parts, but I find that acceptable in such an adventurous work. (The Wikipedia article on the book manages to give a sense of what went on between its covers, and mentions SR as well.)
The SR aspect comes about because Hofstadter feels that it may be central to the workings of consciousness, or at least central to one way of understanding it, which shouldn’t be too surprising since we think of consciousness as self-awareness. Bringing in SR for the sake of consciousness then explains why Kurt Gödel should get woven into the book: Gödel’s notorious “incompleteness theorems” is the great mathematical example of SR, not to mention possibly the pinnacle of modern mathematical thought.
Gödel published his results in 1931, not so long after Alfred Whitehead and Bertrand Russell published their Principia Mathematica (1910–1913). Their goal was to develop an axiomatic basis for all of number theory. They believed they had done it, but Gödel’s result proved that doing what they thought they’d done was impossible. How devastating! (More Wikipedia to the rescue: about Whitehead & Russel’s PM, and about Gödel’s Incompleteness Theorems.)
Gödel’s result says (in my words) that any sufficiently complex arithmetical system (i.e., the system of PM, which aimed to be complete) is necessarily incomplete, meaning that there are self-consistent statements of the system that can be made that are manifestly true but yet are unprovable within the system, which makes it incomplete, or that there are false statements that can be proven, which makes it inconsistent. Such statements are known as formally undecidable propositions.
This would seem to straying pretty far from SR and consciousness, but hold on. How did Gödel prove this remarkable result?# The proof itself was the still-more remarkable result. Gödel showed how one could construct a proposition within the confines of the formal system, which is to say using the mathematical language of the arithmetical system, that said, in effect, “I am a true statement that cannot be proven”.
Pause to consider this SR proposition, and you’ll see that either 1) it is true that it cannot be proven, which makes it a true proposition of the formal system, therefore the formal system is incomplete; or 2) it can be proven, in which case the proposition is untrue and the formal system in inconsistent (contradictory). Do you feel that sinking, painted-into-the-corner feeling?
Of course, it’s the self-reference that causes the whole formal system to crumble. Suddenly the formal system is battling a paradox hemorrhage that feels rather like the Liar’s Paradox (“All Cretans are liars”) meets Russell’s own Barber Paradox (“the barber shaves all those in the town who do not shave themselves; who shaves the barber?”). When these things hit my brain it feels a little like stepping between parallel mirrors, or looking at a TV screen showing its own image taken with a TV camera: instant infinite regress and an intellectual feeling of free-fall.
Does Gödel’s Incompleteness Theorems and SR have anything to do with consciousness? Well, that’s hard to say, but that wasn’t Hofstadter’s point, really. Instead, he was using SR and the Incompleteness Theorems as metaphors for that nature of consciousness, to try to get a handle on how it is that consciousness could arise from a biologically deterministic brain, to take a reductionist viewpoint.
At about the same time I read GEB for the second time, I remember having a vivid experience of SR in action. I was reading a book, Loitering with Intent, by the extraordinary Muriel Spark (about whom more later someday). It is a novel, although at times one identifies the first-person narrative voice with the author. There came a moment about mid-way through the book when the narrator was describing having finished her book, which was in production with her publisher, how she submitted to having a publicity photograph taken for use on the back jacket of the book.
The description seemed eerier and eerier until I was forced to close the book for a moment and stare at the photograph on the back jacket. It mirrored exactly what had happened in the text, which was fiction, unless of course it wasn’t, etc. Reality and fiction vibrated against each other like blue printing on bright-orange paper. It was another creepy hall-of-mirrors moment, but also felt a moment of unrivaled verisimilitude. I think it marked the beginning of my devotion to Dame Muriel.
And that’s what this article is about. I suppose I could have used “untitled” as the title, but I’ve never figured out whether “untitled” is a title or a description. I think “undescribed” might be a still-bigger problem, though.
Now, on to the one-thousand-and-first.%
———-
* You’ll notice that neither the first nor the thousandth have serial numbers that correspond; the first is numbered “2″, the thousandth is numbered “1091″. Clearly I do not publish every article that I begin, evidently discarding, on average, about 9% of them. Some get started and never finished, and some seem less of a good idea when I’m finished with them than when I started.
# And please note, this is mathematically proven, it is not a conjecture.
% I’ve been reading stuff lately that described how arabic numerals were only adopted in the 15th century; can you imagine doing arithmetic with spelled-out numbers! Not only that, but before the invention of double-entry bookkeeping–also in the 15th century–and sometimes even after, business transactions were recorded in narrative form. Yikes!
Feb
13
Posted by jns on
February 13, 2008
The website GetReligion discusses press coverage of news stories about religion, and how well they exhibit an understanding of the religious issues involved. Their name comes from the idea that “The press…just doesn’t get religion.”
Well, in this little example I’m afraid there’s a bit of a need for some GetMath. In a story called “Define social justice — give at least one example“, Mark Stricherz is discussing a story about Jeremiah Wright Jr., the pastor of the church Barack Obama belongs to. I have no issues with the analysis, just with this excerpt
As Ramirez noted, plainly but aptly,
“Obama was one of the thousands who joined Trinity under Wright’s leadership. When Wright became Trinity’s pastor in 1972, the church had 85 members. Today, Trinity has a congregation of 8,500, with more than 80 ministries, making it one of the largest and most influential black churches in the nation.”
In other words, during his tenure Wright’s congregation increased by more than 1,000 percent.
Of course, one notes that Wright’s congregation increased by well over well over 1,000%. In fact, it increased by 10,000%. In other words, it increased by a factor of 100.
To move from a fractional factor, say 0.45, to an expression in percent, one multiplies by 100. Thus, 0.45 of something is also said to be 45% of that something. To move from an expression in percent to a decimal fraction, divide the percent figure by 100. Thus, 32% of something is 0.32 times that something.
This works even if the fractional part is greater than the something being compared to, it’s just that the decimal expression is greater than 1, and the percent expression is greater than 100%. This general expression
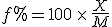
where 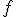 is the percent expression,
is the percent expression, 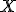 is what I’ve called the fractional part, and
is what I’ve called the fractional part, and 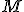 is the amount being compared to, works regardless of whether the “quantity” is greater than or less than the “comparison” value.
is the amount being compared to, works regardless of whether the “quantity” is greater than or less than the “comparison” value.
So, in Mr. Wright’s case, his congregation, in going from 85 to 8,500 increased by a factor of 100, or by
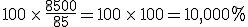
I expect Mr. Stricherz knows this and simply mistyped, but it did provide me an excuse for a little pedantic moment of the type I love so much.
Feb
09
Posted by jns on
February 9, 2008
More catching up. Months ago I finished reading Steven Vogel’s Cat’s Paws and Catapults : Mechanical Worlds of Nature and People (New York : W.W. Norton & Company, 1998, 382 pages). I enjoyed it immensely. Here’s my book note.
This book comes with a confession on my part, all about judging a book by its cover. I bought my copy of the book at my local library’s book store, for $1. Evidently it had been donated to the library (a name is written inside the cover). Good value and it makes it worth taking the risk that the book might not be top notch. Because of that, and because the title + subtitle seemed a little over the top to me, I feared that the book would be a light-weight, pop-journalism contribution to the currently fashionable topic of biomechanics, or bioengineering, or bio-something-or-other.
Now, pop-journalistic treatments are not a bad thing–at least, I don’t object so long as the pop-journalist pays some attention to scientific accuracy. For instance, I mostly enjoyed reading Peter Forbes’ The Gecko’s Foot : Bio-Inspiration : Engineering New Materials from Nature (book note) and didn’t find it scientifically irritating, although I felt that it could have been more than it was. It would suit other people’s taste quite nicely. I think my fear was that I found the proposed topic quite appealing and worried that the writing might be annoyingly breezy.
Well, I was wrong about Mr. Vogel, so I want to apologize to him here. His book was admirable and met my requirements for outstanding scienticity quite handily. Despite its high density of analytical insight and bioengineering understanding, I found it quite engaging and pleasant to read, just not a fast read.
Now, on to the left-over excerpt. You may recall, if you were paying very close attention, that I have a nostalgic fascination with the “Hedge-Apple”, or “Osage Orange” tree, and wrote about that once. In that piece I came upon the extraordinary statement:
The widespread planting of Osage-orange stopped with the introduction of barbed wire.
and didn’t bother to explain it very thoroughly.
Well, here is Mr. Vogel on the hedge-apple and the introduction of barbed wire, to lay it all out for us:
Barbed Wire. Keeping livestock pinned within hedgerows of thorny plants is an old practice, one especially useful where wood or stone for fencing is in short supply. Settlers of the North American prairies faced an ever-worsening wood shortage as they moved westward. The plant of choice for the Midwest was a shrubby tree native to East Texas and nearby areas–the Osage orange (Maclura pomifera)–and a small industry during the 1860s and 1870s supplied its seeds and seedlings for use farther north. This thorny bush, though, had substantial disadvantages. Growing an effective hedge took about three years, the grapefruit-size but inedible fruits were a nuisance, and the hedge was both immovable and a nuisance to maintain. Michael Kelly’s patent of 1868 for an early form of barbed wire was explicit: “My invention [imparts] to fences of wire a character approximating to that of a thorny hedge. I prefer to designate the fence so produced as a thorny fence.” Indeed, the wire was produced by an enterprise called the Thorn Wire Hedge Company, perhaps advertising its utility by drawing attention to a familiar antecedent. Figure 12.10 shows the similarity of plant thorns such as those ont he Osage orange to this early form of barbed wire.
Kelly barbed wire was eclipsed by two competing brands of cheaper wire after 1874; as with wings, spinnerets, and telephone transmitters [examples previously discussed as inventions inspired by nature], fidelity to nature guarantees no economic magic. Patents for the new types were held by Joseph Glidden and Jacob Haish. With the usual personification of invention, Joseph Glidden is often listed as the inventor of barbed wire. Haish, almost certainly not coincidentally, had a lumberyard that sold Osage orange seed. As the historian George Basalla puts it, “barbed wire was not created by men who happened to twist and cut wire in a peculiar fashion. It originated in a deliberate attempt to copy an organic form that functioned effectively as a deterrent to livestock.” Barbed wire has been an enduring success. Current consumption in the United States runs to well over a hundred thousand tons a year. [pp. 266--267]
Feb
07
Posted by jns on
February 7, 2008
In a recent comment to a post I made about reading Chet Raymo’s book Walking Zero, Bill asked an interesting question:
Jeff, there’s a question that has always bothered me. Raymo’s talk about the Hubble Space Telescope’s Ultra Deep Field image (page 174) raised it for me again. I’m sure you have the answer, or the key to the flaw in my “reasoning,” such as it is. The most distant of the thousands of galaxies seen in that image is 13 billion light years away. “The light from these most distant galaxies began its journey when the universe was only 5 percent of its present age” (174-175), and presumably only a small proportion of its present size. Now, the galaxies are speeding away from each other at some incredible speed. So if it has taken 13 billion years for light to come to us from that galaxy where it was then (in relation to the point in space that would become the earth at a considerably later date), how far away must it be now? Presumably a lot farther away than it was then?
Before we talk about the universe, I do hope you noticed that the background image I used for the “Science-Book Challenge 2008″ graphic, which you will see at right if you are reading this from the blog site (rather than an RSS feed), or which you can see at the other Science-Book Challenge 2008 page, is actually part of the Hubble Deep-Field image. If you follow the link you can read quite a bit about the project, which was run from the Space Telescope Science Institute (STScI), which is relatively nearby, in Baltimore. It’s the science institute that was established to plan and execute the science missions for the HST; flight operations are handled at Goddard, which is even closer, in Greenbelt, Maryland.
Now let’s see whether we have an answer to Bill’s question.
I think you may be able to resolve the quandary if you focus on the distance of the object seen, rather than when the light through which we see it left its bounds.
The object’s distance is the thing that we can determine with reasonable accuracy (and great precision) now, principally through measuring red shifts in spectra of the object.* One of astronomer Hubble’s great achievements was determining that the amount of red-shift, which depends on our relative velocity, corresponds directly with the distance between us and the observed object.# So, take a spectrum, measure the red shift of the object, and you know more-or-less exactly how far away it was when the light left it.
Oh dear, but that doesn’t really settle the issue, does it? On the other hand, it may be the most precise answer that you’re going to get.
Saying that, when the light left the object, the universe was only 5% its current size should be seen more as a manner of speaking than a precise statement. It can be a rough estimate, along these lines. Say the universe is about 14 billion years old and this object’s light is 13 billion years old, and if the universe has been expanding at a uniform rate, the the universe must have been (14-13)/14ths or about 7% its current size (which is about 5% its current size).
But I’d say you should treat that just as something that makes you say “Wow! That was a long time ago and the universe must have been a lot different”, and don’t try to extrapolate much more than that.
It’s probably true that the universe hasn’t been expanding at a uniform rate, for one thing. There’s a theory that has had some following for the past 25 years, called the theory of inflation.** For reasons that have to do with the properties of matter at the extreme compression of the very, very early universe, the theory suggests that there was an “inflationary epoch” during which the universe expanded at a vastly faster rate than is visible currently. Now, some of the numbers involved are astonishing, so hold on to your seat.
The inflationary epoch is thought to have occurred at a time of about 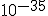 seconds after the big bang, and to have lasted for about
seconds after the big bang, and to have lasted for about 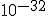 seconds.## During this time, it is thought that the universe may have expanded by a factor of
seconds.## During this time, it is thought that the universe may have expanded by a factor of 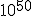 . (One source points out that an original 1 centimeter, during inflation, became about 18 billion light years.)
. (One source points out that an original 1 centimeter, during inflation, became about 18 billion light years.)
So, inflation would rather throw a kink into the calculation, not to mention the possibility that the universe is not expanding in space, but that space itself is expanding. That can make calculations of what was where when a touch trickier.
But that’s not the only problem, of course. I can hear Bill thinking, well, that may all be so, but if we’re seeing the distant object as it was 18 billion light years ago, what’s it doing now.
I’m afraid that’s another problem that we’re not going to resolve, and not for lack of desire or know-how, but because of physical limitation. The bigger, tricker issue is — and I almost hate to say it — relativity. No doubt for ages you’ve heard people say of relativity that it imposes a universal speed limit: the speed of light. Nothing can go faster than the speed of light. That’s still true, but there’s an implication that’s not often spelled out: the breakdown of simultaneity, or what does it mean for thing to happen at the same time?
It’s not usually a tricky question. Generally speaking, things happen at the same time if you see them happen at the same time. Suppose you repeat Galileo’s famous experiment of dropping two different weights from the leaning tower of Pisa at the same time (he said he would), and you observe them hitting the ground at the same time. No real problem there: they fell right next to each other and everyone watching could see that they happened at the same time.
Suppose the objects are not next to each other though. Suppose instead that we observe some event, say, a meteor lands in your front yard. 8.3 minutes later you observe a solar flare on the sun through your telescope. “Isn’t that interesting,” you say, “since the Earth is 8.3 light-minutes from the Sun, that flare and my meteor’s landing happened at the same time.”
Well, the problem here, as you may have heard about before, is that an observer traveling past the Earth at very high speeds and using a clock to measure the time between the two events, your meteor and the solar flare, would deduce that the two events did not happen at the same time. The mathematics is not so difficult, but messy and probably not familiar. (You can see the equations at this page about Lorentz Transformations, or the page about Special Relativity.)
What happens is that in order for the speed of light to be constant in all inertial reference frames–the central tenet of special relativity–causality breaks down. Events that appear simultaneous to one observer will, in general, not appear simultaneous to another observer traveling at a uniform velocity relative to the first observer. (This cute “Visualization of Einstein’s special relativity” may help a little, or it may not.) Depending on the distance between two events, different observers may not even agree on with event happened first.
So, the not-so-satisfactory answer, Bill, is a combination of 1) because of inflation, it may not be so very much further away than it was 13 billion years ago; but 2) because of the breakdown of simultaneity due to special relativity, we can’t say what it’s doing now anyway, because there is no “now” common to us and the object 13 billion light-years away.%
Gosh, I do hope I answered the right question!
———-
* You may recall that red shift refers to the Doppler effect with light: when objects move away from us, the apparent wavelength of their light stretches out–increases–and longer wavelengths correspond to redder colors, so the light is said to be red-shifted. This happens across the entire electromagnetic spectrum, by the way, and not just in the visible wavelengths.
# Applying Hubble’s Law involves use of Hubble’s Constant, which tells you how fast the expansion is occurring. The curious thing about that is that Hubble’s Constant is not constant. I enjoyed reading these two pages: about Hubble’s Law and Hubble’s Constant. The second one is rather more technical than the first, but so what.
**Two useful discussions, the first shorter than the second: first, second.
## Yes, if you want to see how small a fraction of a second that was, type a decimal point, then type 31 zeroes, then type a “1″.
% I leave for the interested reader the metaphysical question of whether this statement means that universal, simultaneous “now” does not exist, or that it is merely unknowable.
Feb
06
Posted by jns on
February 6, 2008
A while back, someone ended up at a page on this blog by asking Google for “the temperature at which the Celsius scale and Fahrenheit scale are the same number”. I don’t think they found the answer because I’d never actually discussed that question1, but I thought the question was pretty interesting and discussing the answer might be a bit of good, clean rocket-science fun.
Actually, there is a prior question that I think is interesting, namely: how do we know that there is a temperature where the Celsius and Fahrenheit scales agree? The answer to that question is related to a simple mathematical idea.2 We can picture this mathematical idea by drawing two lines on a chalkboard (or whiteboard) with a rule.
First, draw line A any way you want, but make it more horizontal than vertical, just to keep things clear. Now, draw line B in such a way that it’s point farthest left is below line A, but its point farthest right is above line A. What you will always find that that line B and line A will cross at some point. This may seem like an obvious conclusion but it is also a very powerful conclusion. Now, knowing where they will cross is another, often more difficult, question to answer.
How do we know, then, that the Fahrenheit and Celsius lines cross? Well, the freezing point of water, say, on the Celsius scale is 0°C, and on the Fahrenheit it is 32°F. On the other hand, absolute zero is -273.15°C, but -459.67°F. So, at the freezing point of water the Fahrenheit line is above the Celsius line, but at absolute zero that situation is reversed.
Finding the point where they cross is a simple question to answer with algebra. The equation that converts Fahrenheit degrees into Celsius degrees is
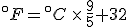
The equation that goes the other way is
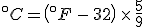
To find the temperature where the two lines cross, take one of the equations and set
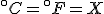
so that
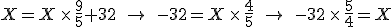
and then solve for 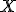 . The result is that
. The result is that
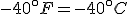
[Addendum: 19 February 2008, for the Kelvin & Fahrenheit folks]
The Kelvin scale of temperatures is a thermodynamic temperature scale: it’s zero point is the same as zero temperature in thermodynamic equations. It used Celsius-sized degrees, and there is indeed a temperature at which the Kelvin and Fahrenheit scales cross. The relation between the two is
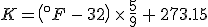
(Note that the absolute temperature scale uses “Kelvins” as the name of the units, and not “degrees Kelvin”.) As in the Fahrenheit / Celsius example, set 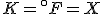 and solve for
and solve for 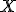 , with the result that
, with the result that
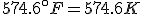
As before, Fahrenheit degrees are larger than Kelvins and will eventually overtake them, but the initial difference between the zero points is much larger, so the crossing point is at a much higher temperature.
———-
1Because of the way links on blogs select different combinations of individual posts, by days, by months, by topics, etc., internet search engines often present the least likely links as solutions to unusual word combinations in search strings. I find this phenomenon endlessly fascinating.
2The mathematical idea is one that I’ve always thought was a “Fundamental Theorem of [some branch of mathematics]“, but I’ve forgotten which (if I ever knew) and haven’t been able to identify yet. This is probably another effect of encroaching old-age infirmity.
I imagine — possibly remember — the theorem saying something like:
For a continuous function 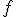 defined on the interval
defined on the interval ![[a,b] [a,b]](http://scienticity.net/sos/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.gif) , for
, for 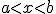 ,
, 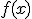 takes on all values between
takes on all values between 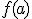 and
and 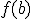 .
.
Feb
03
Posted by jns on
February 3, 2008
Thermodynamics is the theory that deals with heat and heat flow without reference to the atomic theory; it was developed at the same time as the steam engine and the family resemblances are striking. All concepts about temperature and pressure in terms of our perceptions of atomic or molecular motion came later and properly belong in the discipline known as Statistical Mechanics.
Awhile back I read this bit in the referenced book and thought it shed a lot of light on the idea of entropy, about which more after the excerpt.
Clausius saw that something was being conserved in Carnot’s [concept of a] perfectly reversible engine; it was just something other than heat. Clausius identified that quantity, and he gave it the name entropy. He found that if he defined entropy as the heat flow from a body divided by its absolute temperature, then the entropy changes in a perfectly reversible engine would indeed balance out. As heat flowed from the boiler to the steam, the boiler’s entropy was reduced. As heat flowed into the condenser coolant, the coolant’s entropy increased by the same amount.
No heat flowed as steam expanded in the cylinder or, as condensed water, it was compressed back to the boiler pressure. Therefore the entropy changed only when heat flowed to and from the condenser and the boiler and the net entropy was zero.
If the engine was perfectly reversible, it and the surroundings with which it interacted remained unchanged after each cycle of the engine. Under his definition of entropy Clausius was able to show that every thing Carnot had claimed was true, except that heat was conserved in his engine.
Once Carnot’s work had been relieved of that single limitation, Clausius could reach another important result: the efficiency of a perfectly reversible heat engine depends upon nothing other than the temperature of the boiler and the temperature of the condenser.
[John H. Lienhard, How Invention Begins (Oxford : Oxford University Press, 2006) p. 90]
Amazing conclusion #1: virtually everything about heat flowing from a warm place to a cool place depends only on the difference in temperature between the warm place and the cool place.
Amazing conclusion #2: there is an idea, call it entropy, that encapsulates #1. If we let 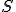 stand for entropy, and
stand for entropy, and 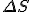 stand for the change in entropy, then we can write
stand for the change in entropy, then we can write
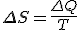
This is Clausius’ definition in symbols.
Now, there’s a lot of philosophical, interpretative baggage that travels with the idea of entropy, but if you can keep this simple approach in mind you can save a lot of heartburn pondering the deeper meaning of entropy and time’s arrow and the heat-death of the universe.
Entropy is an accounting tool. When heat flows between the hot place and the cold place, at best, if you allow it very carefully, you may be able to reverse the process but you will never do better, which means that you will never find the cold place getting colder than originally, nor the hot place getting hotter than originally, no matter what you do, unless you put still more heat into the system.
That’s one version of the notorious “Second Law of Thermodynamics”. There are a number of other forms.
For instance, another way of saying was I just said: entropy never decreases. There, thermodynamic accounting made easy.
Another one that’s useful: if you construct a device that uses heat flowing from a hot place to a cold place to do mechanical work — say, in a steam engine — some of the heat is always wasted, i.e., it goes into increasing entropy. Put another way: heat engines are never 100% efficient, not because we can’t build them but because it is physically impossible.
Think for a moment and you’ll see that the implication of this latter form of the Second Law of Thermodynamics is a statement that perpetual motion machines are impossible. They just are, not because a bunch of physicists though it might be a good idea to say it’s impossible, but because they are. That’s the way the universe is made.
Entropy needn’t be scary.
———-
* 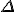 is a general purpose symbol often used to indicate a change in the quantity represented by the letter following it.
is a general purpose symbol often used to indicate a change in the quantity represented by the letter following it.
 This week’s beard belongs to Albrecht Dürer, easily in my top-10 of most extraordinary artists ever. This amazing self-portrait was painted when the artist was 29 years old, in the year 1500. Is it symbolic that Dürer paints himself in this remarkably self-possessed, self-confident pose, looking directly at the viewer? It’s also interesting that he paints himself more as an aristocrat rather than with the commonly affected palette in hand, as a painter. What is the power in this painting that makes it feel so much as though it communicates directly with the viewer across the more than five centuries since Dürer painted it. Honestly, it creates for me a frisson that very few works of art manage to do.
This week’s beard belongs to Albrecht Dürer, easily in my top-10 of most extraordinary artists ever. This amazing self-portrait was painted when the artist was 29 years old, in the year 1500. Is it symbolic that Dürer paints himself in this remarkably self-possessed, self-confident pose, looking directly at the viewer? It’s also interesting that he paints himself more as an aristocrat rather than with the commonly affected palette in hand, as a painter. What is the power in this painting that makes it feel so much as though it communicates directly with the viewer across the more than five centuries since Dürer painted it. Honestly, it creates for me a frisson that very few works of art manage to do.
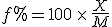
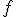 is the percent expression,
is the percent expression, 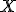 is what I’ve called the fractional part, and
is what I’ve called the fractional part, and 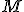 is the amount being compared to, works regardless of whether the “quantity” is greater than or less than the “comparison” value.
is the amount being compared to, works regardless of whether the “quantity” is greater than or less than the “comparison” value.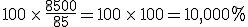
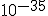 seconds after the big bang, and to have lasted for about
seconds after the big bang, and to have lasted for about 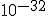 seconds.## During this time, it is thought that the universe may have expanded by a factor of
seconds.## During this time, it is thought that the universe may have expanded by a factor of 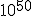 . (One source points out that an original 1 centimeter, during inflation, became about 18 billion light years.)
. (One source points out that an original 1 centimeter, during inflation, became about 18 billion light years.)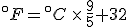
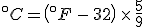
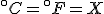
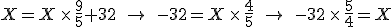
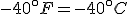
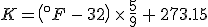
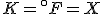 and solve for
and solve for 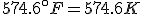
![[a,b] [a,b]](http://scienticity.net/sos/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.gif) , for
, for  ,
, 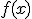 takes on all values between
takes on all values between 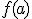 and
and 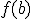 .
.
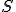 stand for entropy, and
stand for entropy, and 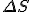 stand for the change in entropy, then we can write
stand for the change in entropy, then we can write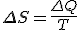
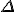 is a general purpose symbol often used to indicate a change in the quantity represented by the letter following it.
is a general purpose symbol often used to indicate a change in the quantity represented by the letter following it.