The Pendulum Swings

Posted by jns on 30 January 2008

Sometimes I’m just reading, minding my own business, when the oddest things smack me squarely in the forehead. For instance:

As believers in faith and ritual over science, perhaps it’s not surprising that they [Evangelical Christians, as it turns out] failed to heed the basic laws of physics.

Most people understand that when a pendulum is pushed too far in one direction, it will eventually, inexorably swing back just as far to the opposite side. This is the natural order of things, and it tends to apply across the board — even to that bulwark of chaos theory, politics.

[Chez Pazienza, "Losing Their Religion", Huffington Post, 30 January 2008]

Whatever is this person talking about and where did s/he get the crazy notions about “the basic laws of physics” on display in these few sentences? (It seems about as nonsensical to me as people who use “literally” to mean “really, really metaphorically”.)

Based on the laws of physics, I believe that a pendulum is a physical object that swings back and forth, often used to keep time. I also believe that if it’s pushed far enough in one direction is will eventually break or, at the very least, enter a non-linear mode of oscillations. In my book, it is in the nature of pendula, even when swung a little in one direction, to swing in the other direction, and then back again in the original direction.

It is this oscillatory nature of the pendulum that is referred to in the metaphorical pendulum of politics and public opinion. Perhaps our author is thinking of a spring that, when squeezed, or stretched, in one direction will spring back just as far in the opposite direction?

As for politics being the bulwark of chaos theory — WTF? Someday, perhaps when we have more time, we’ll talk about some interesting history and results in chaos studies, but I don’t think politics will get mentioned, alas.

A pendulum is a fascinating thing, of course. Its use in clocks as a timing governor^* is traced to Galileo’s observation that the period of oscillation depends only on the length of the pendulum and not on the amplitude of its swing. The period (“T”) depends only on the length (“L”) of the pendulum and the acceleration due to gravity (“g”–a constant number):

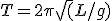
Now, this is really an approximation with some assumptions like a) the pendulum has all its weight at the swinging end; and b) the amplitude of the swing isn’t too big. But it’s really a very good approximation, good enough for very precise horological instruments.

This equation tells us a couple of interesting things. One is that, because of the square-root sign over the length, if you want to double (multiply by 2) the period of a pendulum you must increase its length by 4; likewise, for half the period make the length one-fourth the original.

This also tells us that tall-case clocks tend to be much the same size. Generally speaking, they are constructed to house a pendulum with a two-second period, i.e., a pendulum that takes precisely one second to swing either way, or one second per tick, one second per tock. The length of such a pendulum is very nearly 1 meter.

At our house we also have a mantel clock that is, not surprisingly, a little under 12 inches tall because it has a pendulum with a period of 1 second, i.e., one second for a complete back-and-forth swing; such a pendulum has a length of about 0.25 meters, or one-quarter the tall-case clock’s pendulum.

Many tall-case clocks that I’ve seen have a pendulum whose rod is actually made from a flat array of a number of small rods, usually in alternating colors. This is a merely decorative vestige of the “gridiron pendulum” invented by master horologist John Harrison in 1720. The pendulum is constructed of two types of metal arranged so that the thermal expansion of one type of metal is compensated for by the thermal expansion of the other. (It’s easiest to look at an illustration, which is discussed here.)
———-
^* The pendulum, coupled with an escapement mechanism, is what allows a pendulum clock to tick off uniform intervals in time.