A Big Piece of Pi

Posted by jns on 22 September 2007

How innocently it all begins, sometimes. For some reason a day or two ago I decided I would take a few google-moments and look into modern computational formulæ that are use to calculate the value of . What a loaded question that turned out to be! Before I’d reached a point to pause and write — and I’m not confident that I’m there yet — I’ve read several mathematics papers, installed software so that I could type equations in the blog [1], thought more about number theory and complex analysis than I have for years, and even gave Isaac a short lecture on infinite series with illustrative equations written on the Taco Bell tray liner. Poor Isaac.

Suppose you want to calculate the value of . The number , you may recall, is transcendental and therefore irrational — serious categories of numbers whose details don’t matter much except to remember that , written as a decimal number, has digits after the decimal point that never repeat and never end. Most famously relates the diameter of a circle, 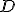, to its radius, 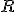, in this manner:

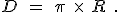
There are also a surprising number of other mathematical equations involving that have no obvious relationship with circles. One very important and useful type of relationship involves infinite series. Infinite series are written in a very compact mathematical notation that will look very inscrutable if it’s unfamiliar, but don’t be alarmed, please, because the idea is relatively simple. Here’s an example:

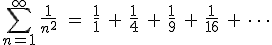
The big greek letter, capital sigma (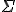), is the symbol that signals the series operation. The letter 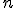underneath the sigma is the index. The index is set in sequence to a series of integer values, in this case starting at one (because 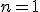), and ending with infinity, as specified by the number on top. Then, for each value of 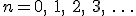, the letter 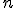is replaced with that number in the mathematical expression following the big sigma and the successive terms are added together, the operation suggested by the sequence of fractions following the equals sign. (Feel free to look at the equation and think about it and look and think, if it’s new to you. Mathematics is rarely meant to be read quickly; it takes time to absorb.)

The other important idea about the series that we have to look at is the idea of convergence, a property of the series meaning that as one adds on each new term the result (called the partial sum, for obvious reasons) gets closer and closer to some numerical value (without going over!). It is said to converge on that value, and that value is known as the limit of the successive partial sums. [2]

Provided that the series converges, the limit of the partial sums is usually treated simply as the value of the series, as thought one could indeed add up the infinite number of terms and get that value.

It turns out that the series we wrote above (the solution to the so-called “Basel problem”) does indeed have a value (i.e., the partial sums converge to a limit) — a rather remarkable value, actually, given our interest in :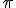

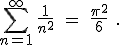
Really, it does. [3]

This equation also gives us a good hint of how the value of is calculated, in practical terms, and this has been true since at least the time of Newton, whether one is calculating by hand or by digital computer. One finds a convenient expression that involves an infinite series on one side of the equals sign and on the other side and starts calculating partial sums. The trick is to find a particularly clever series that converges quickly, so that each new term added to the partial sum gets you closer to the limit value as fast as possible.

It should come as no surprise that there are an infinite number of equations involving with reasonable convergence properties that could be used to calculate its value, and an astounding number that have actually been used to do that. [4]

It may also be no great surprise to hear that new equations are discovered all the time, although a new type of equation is rather more rare. Now, this part is a bit like one of those obscure jokes where we have to have some background and think about it before we get it. [5]

This is where my innocent investigation into calculating took an unexpected turn. Let me quote the fun introduction to a paper by Adamchik and Wagon [6] :

One of the charms of mathematics is that it is possible to make elementary discoveries about objects that have been studied for millenia. A most striking example occurred recently when David Bailey of NASA/Ames and Peter Borwein and Simon Plouffe of the Centre for Experimental and Computational Mathematics at Simon Fraser University (henceforth, BBP) discovered a remarkable, and remarkably simple new formula for . Here is their formula:

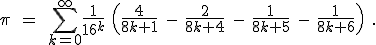
The original paper in which Bailey, Borwein, and Plouffe published this result appeared in 1997. [7]

Don’t freak out, just breathe deeply and look at it for a bit. [8] How they came by this equation is an interesting story in itself, but not one to go into here. It’s enough to know that it can be proven to be correct. (In fact, Adamchik and Wagon actually say “The formula is not too hard to prove…”; if you didn’t read note #5, now would be a good time!)

Isn’t it remarkable looking! I saw it and my reaction was along the lines of “how could ever be equal to that thing?” This thing, by the way, is referred to as the “BBP formula” or the “BBP algorithm”. And then the talk about this equation started to get a little weird and my original train of through about how to calculate derailed.

People wrote about the BBP algorithm in very admiring terms, like “the formula of the century”, which started to sound like hyperbole, but really wasn’t. Then I tripped over some statements like this one [9] :

Amazingly, this formula is a digit-extraction algorithm for in base 16.

Now, there’s a statement I had to pause and think for awhile to make some sense out of.

The “base 16″ part was easy enough. Usually we see the decimal expansion of written in our everyday base 10 (this is truncated, not rounded):

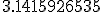
In base 16 the expansion looks like this (also truncated) [10] :

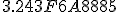
In the same way that the digits after the decimal point in the base-10 expansion means this:

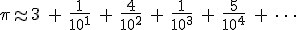
the hexadecimal expansion means simply this:

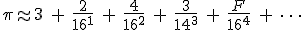
where the hexadecimal digits “A, B, C, D, E, and F” have the decimal values “10, 11, 12, 13, 14, and 15″.

For quite awhile I didn’t get the notion that it was a “decimal extraction algorithm”, which I also read to mean that this algorithm could be used to compute the 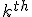digit in the hexadecimal representation without calculating all the preceding digits.

Now, that’s an amazing assertion that required understanding. How could that be possible. You’ve seen enough about series formulæ for to see that the way one calculates is to keep grinding out digits until you get to, say, the millionth one, or the billionth one, which can take a long time.

If only I had written down first thing the equation I wrote down above for how the various hexadecimal digits add together as the numerators of powers of (1/16), it would have been obvious. Look back now at the BBP equation. See that factor

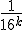
that comes right after the big sigma? That’s the giant clue about the “digit-extraction” property. If the expression in the parentheses happened to be a whole number between decimal values 0 and 15, then the 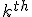term would be exactly the 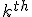digit in the hexadecimal expansion of .

That’s an amazing idea. Now, it’s not exactly the 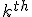digit, because that expression doesn’t evaluate to a whole number between 0 and F (hexadecimal). Instead, it evaluates to some number smaller than 1, but not incredibly smaller than one. (If, e.g., k = 100 it’s about 0.000002).

Philosophically, and mathematically, it’s important that it’s not exactly a digit-extraction algorithm, but an approximate one. You can’t just calculate the millionth digit just by setting k = 1,000,000 and computing one term.

Remarkably enough, though, the BBP algorithm can be, in effect, rearranged to give a rapidly converging series for the millionth digit, if you choose to calculate that particular digit. [11]

Now, in the realm of true hyperbole, I read some headlines about the BBP algorithm that claimed the algorithm suggested that there was some pattern to the digits of and that the digits are not truly random — words evidently meant to be spoken in a hushed voice implying that the mysteries of the universe might be even more mysterious. Bugga bugga!

Now, that business about how maybe now the digits of aren’t random after all — it’s hogwash because the digits of never were random to begin with. It’s all a confusion (or intentional obfuscation) over what “random” means. The number is and always has been irrational, transcendental, unchangeably constant, and the individual digits in the decimal (or hexadecimal) expansion are and always have been unpredictable, but not random.

They cannot be random since has a constant value that is fixed, in effect, by all the mathematical expressions that it appears in. The millionth digit has to be whatever it is in order to make satisfy the constraints of the rest of mathematics. It’s the case that all of the digits are essentially fixed, and have been forever, but we don’t know what their values are until we compute them.

Previously, to know the millionth digit we had to calculate digits 1 through 999,999; with the BBP algorithm that’s not necessary and a shorter calculation will suffice, but that calculation still involves a (rapidly converging) infinite series. Individual digits are not specified, not really “extracted”, but they are now individually calculable to arbitrary precision. And, since individual digits are whole numbers with decimal values between 0 and 15, reasonable precision on calculating the digit tells you what the actual digit is.

Still, it is an amazing formula, both practically and mathematically. And now I just tripped over a paper by the BBP authors about the history of calculating . [12] Maybe I can finally get my train of thought back on track.
———-
[1] At the core is mimeTeX, a remarkable piece of software written by John Forkosh that makes it possible for those of us familiar with TeX, the mathematical typesetting language created some two decades ago by mathematician Donald Knuth, to whip up some complicated equations with relative ease.

[2] This limit is the same concept that is central in calculus and has been examined in great care by anyone who has taken a calculus course, and even more intensively by anyone who’s taken courses in analysis. But, for the present, there’s no need to obsess over the refinements of the idea of limits; the casual idea that comes to mind in this context is good enough.

[3] It was proven by Leonhard Euler in 1735. If you really, really want to see a proof of this assertion, the Wikipedia article on the Basel problem will provide enough details to satisfy, I expect.

[4] The page called “Pi Formulas” at Wolfram MathWorld has a dazzling collection of such equations.

[5] There is an old joke of this type about mathematicians. We used to say “The job of a mathematician is to make things obvious.” This refers to the habit among those professionals of saying “obviously” about the most obscure statements and theorems. Another version of the joke has a mathematician writing lines of equations on a chalkboard during class and reaching a point when he says “it’s obvious that…”, at which point he pauses and leaves the room. The class is mystified, but he returns in 20 minutes, takes up where he left off in his proof, saying “Yes, it is obvious that….”

The version of this that one finds in math and physics textbooks is the phrase, printed after some particularly obscure statement, “as the reader can easily show.” That phrase appeared once in my graduate text on electrodynamic (by J.D. Jackson, of course, for those in the know), and showing it “easily” took two full periods of my course in complex analysis.

[6] Victor Adamchik and Stan Wagon, “: A 2000-Year Search Changes Direction“, Mathematica in Education and Research, vol. 5, no.1, (1996), pp, 11–19.

[7] David Bailey, Peter Borwein, and Simon Plouffe, “On the Rapid Computation of Various Polylogarithmic Constants”, Mathematics of Computation, vol. 66, no. 218 (April 1997), pp. 903–913; reprint available online.

[8] And remember that writing the 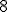next to the 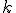just means to multiply them together. Although I used 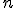as the index in the example above, here the index is called 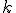— the name doesn’t matter, which is why it’s sometimes called a dummy index.

[9] For an example: Eric W. Weisstein, “BBP Formula“, MathWorld–A Wolfram Web Resource, accessed 23 September 2007 [the autumnal equinox].

[10] “Sample digits for hexa-decimal digits of pi“, 18 January 2003.

[11] If you want to know the details, there’s a nice paper written by one of the original authors a decade later in which he shows just how to do it: David H. Bailey, “The BBP Algorithm for Pi“, 17 September 2006, (apparently unpublished).

[12] David H. Bailey, Jonathan M. Borwein, Peter B. Borwein, and Simon Plouffe, “The Quest for Pi”, Mathematical Intelligencer, vol. 19, no. 1 (Jan. 1997), pp. 50–57; reprint available online.